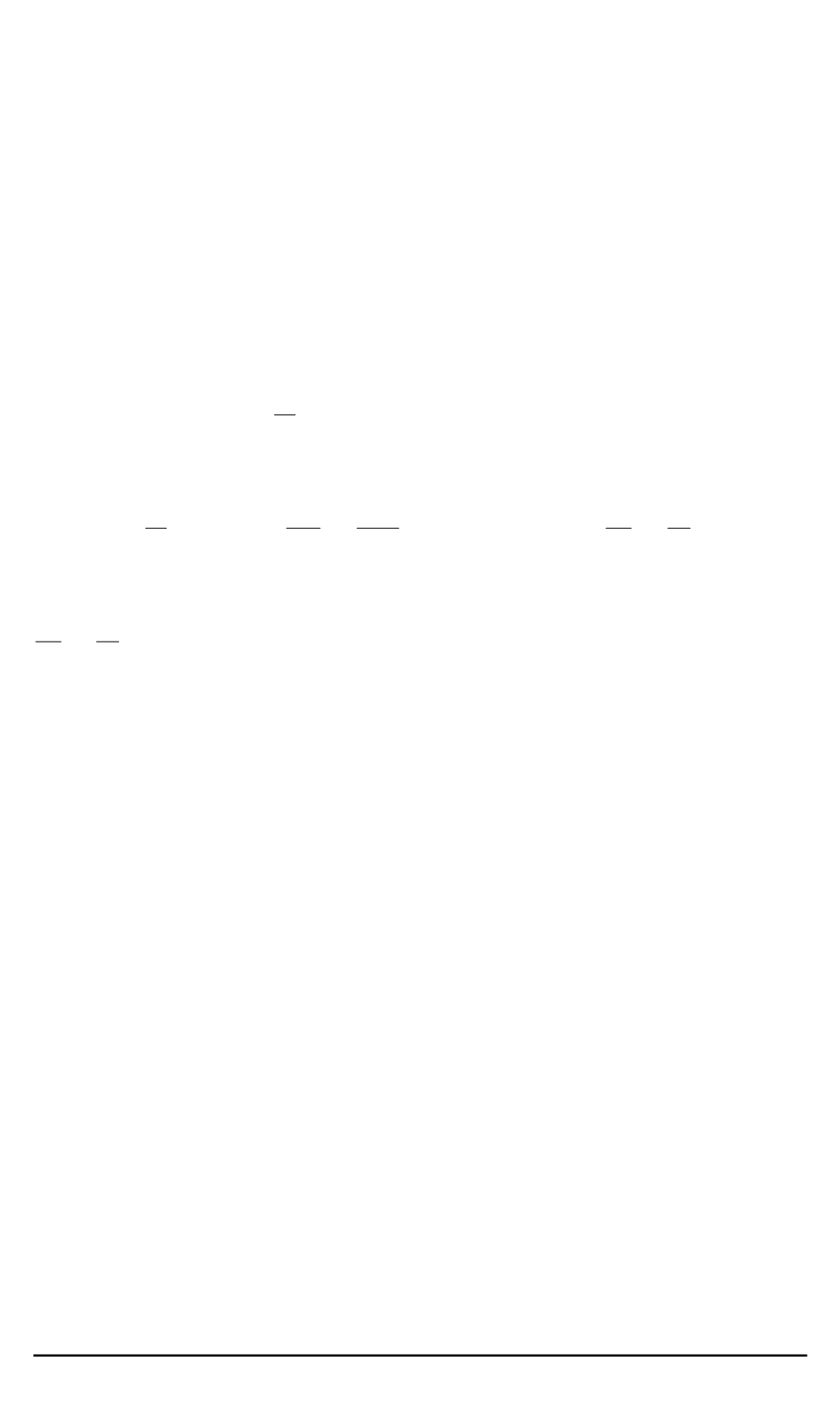
b
6
=
δ
4
1
+
e
11
p p
(
e
12
−
α
12
)
e
13
p
p
(
e
21
−
α
21
)
δ
4
2
+
e
22
p p
(
e
23
−
α
23
)
e
31
p
p
(
e
32
−
α
32
)
δ
4
3
+
e
33
p
.
Характеристическое уравнение (6) должно иметь три пары чисто
мнимых корней. Если произвести замену
λ
2
=
y
, то соответствующее
кубическое уравнение
y
3
+
b
2
y
2
+
b
4
y
+
b
6
= 0
(7)
должно иметь три отрицательных корня. Рассмотрим общую схему
исследования знаков корней кубического многочлена.
Заменой
y
=
y
1
−
b
2
3
это уравнение сводится к следующему:
y
3
1
+
ry
1
+
q
= 0
,
где
r
=
−
b
2
2
3
+
b
4
,
q
=
2
b
3
2
27
−
b
2
b
4
3
+
b
6
. Выражение
r
3
27
+
q
2
4
называют
дискриминантом этого уравнения. По его знаку определяют количе-
ство действительных корней у исходного уравнения (7). При условии
r
3
27
+
q
2
4
<
0
уравнение (7) имеет три различных действительных кор-
ня, если у исходного уравнения все коэффициенты положительны и
выполняется условие Рауса-Гурвица
b
2
b
4
−
b
6
>
0
, то все его корни
отрицательны.
Применив указанную схему исследования к уравнению (6), нахо-
дим такое
p
≈
109
,
986
, что при
0
< p < p
характеристическое урав-
нение (6) имеет три пары чисто мнимых корней. То есть при
0
< p < p
положение равновесия системы устойчиво. Этот результат совпадает
с результатами работы [2], где собственные функции найдены в виде
ряда.
Рассмотрим теперь случай
k >
0
. Характеристическое уравнение
системы (5) принимает следующий вид:
λ
6
+
b
1
λ
5
+
b
2
λ
4
+
b
3
λ
3
+
b
4
λ
2
+
b
5
λ
+
b
6
= 0
,
(8)
где
b
1
=
k
(
δ
4
1
+
δ
4
2
+
δ
4
3
)
,
b
2
=
k
2
(
δ
4
1
δ
4
2
+
δ
4
2
δ
4
3
+
δ
4
1
δ
4
3
) +
δ
4
1
+
δ
4
2
+
δ
4
3
+
p
(
e
11
+
e
22
+
e
33
)
,
b
3
=
k
3
δ
4
1
δ
4
2
δ
4
3
+
k
((
δ
4
1
+
δ
4
2
)(
δ
4
3
+
e
33
p
)+
+ (
δ
4
1
+
δ
4
3
)(
δ
4
2
+
e
22
p
) + (
δ
4
2
+
δ
4
3
)(
δ
4
1
+
e
11
p
))
,
76
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4