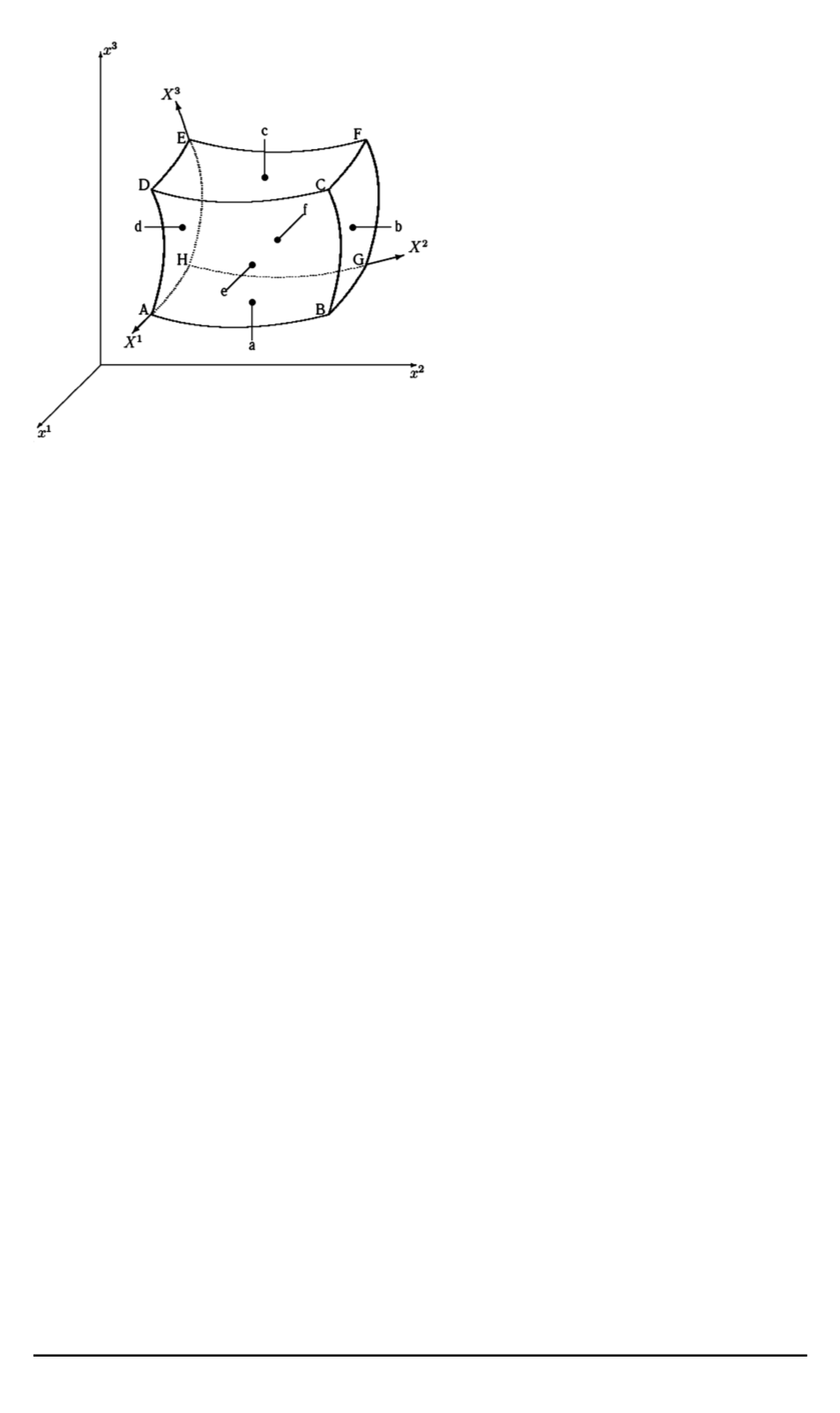
Рис. 1. Адаптивная система координат
Метод ленточных адаптив-
ных сеток
. Для решения урав-
нения (1) с граничными (3)–
(5) и начальными (6) условия-
ми введем для области реше-
ния
V
специальную разност-
ную регулярную сетку, обра-
зованную кубическими криво-
линейными ячейками, которая
называется ленточной адаптив-
ной сеткой (ЛАС). Алгоритм по-
строения ЛАС для трехмерной
области следующий.
Рассматриваемую область
V
разобьем на совокупность
“крупных” криволинейных кубов
V
i
, каждый из которых имеет вид,
изображенный на рис. 1; в настоящей работе расчетная область была
разделена на пять подобластей.
Обозначим в пространстве
R
3
прямоугольные декартовы коорди-
наты
x
i
, а адаптивные координаты —
X
j
. Для генерации адаптивной
разностной сетки необходимо отыскать зависимости
x
i
=
f
i
(
X
j
)
,
(7)
которые преобразуют криволинейный куб в координатах
x
i
в прямоли-
нейный куб
[0
,
1]
×
[0
,
1]
×
[0
,
1]
в координатах
X
j
. Зададим исходную
геометрию — стороны
a
,
b
,
c
,
d
,
e
,
f
(см. рис. 1) каждого криволиней-
ного куба
V
i
в параметрическом виде:
x
i
=
x
i
a
(
X
1
, X
2
)
,
x
i
=
x
i
b
(
X
1
, X
3
)
,
x
i
=
x
i
c
(
X
1
, X
2
)
,
x
i
=
x
i
d
(
X
1
, X
3
)
,
x
i
=
x
i
e
(
X
2
, X
3
)
,
x
i
=
x
i
f
(
X
2
, X
3
)
.
(8)
Искомое преобразование координат (7) имеет вид
f
i
(
X
1
, X
2
, X
3
) =
=
P
i
(
X
1
, X
2
, X
3
)
−
[
P
i
(
X
1
, X
2
,
0)
−
x
i
a
(
X
1
, X
2
)](1
−
X
3
)
−
−
X
3
[
P
i
(
X
1
, X
2
,
1)
−
x
i
c
(
X
1
, X
2
)]
,
(9)
46
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3


