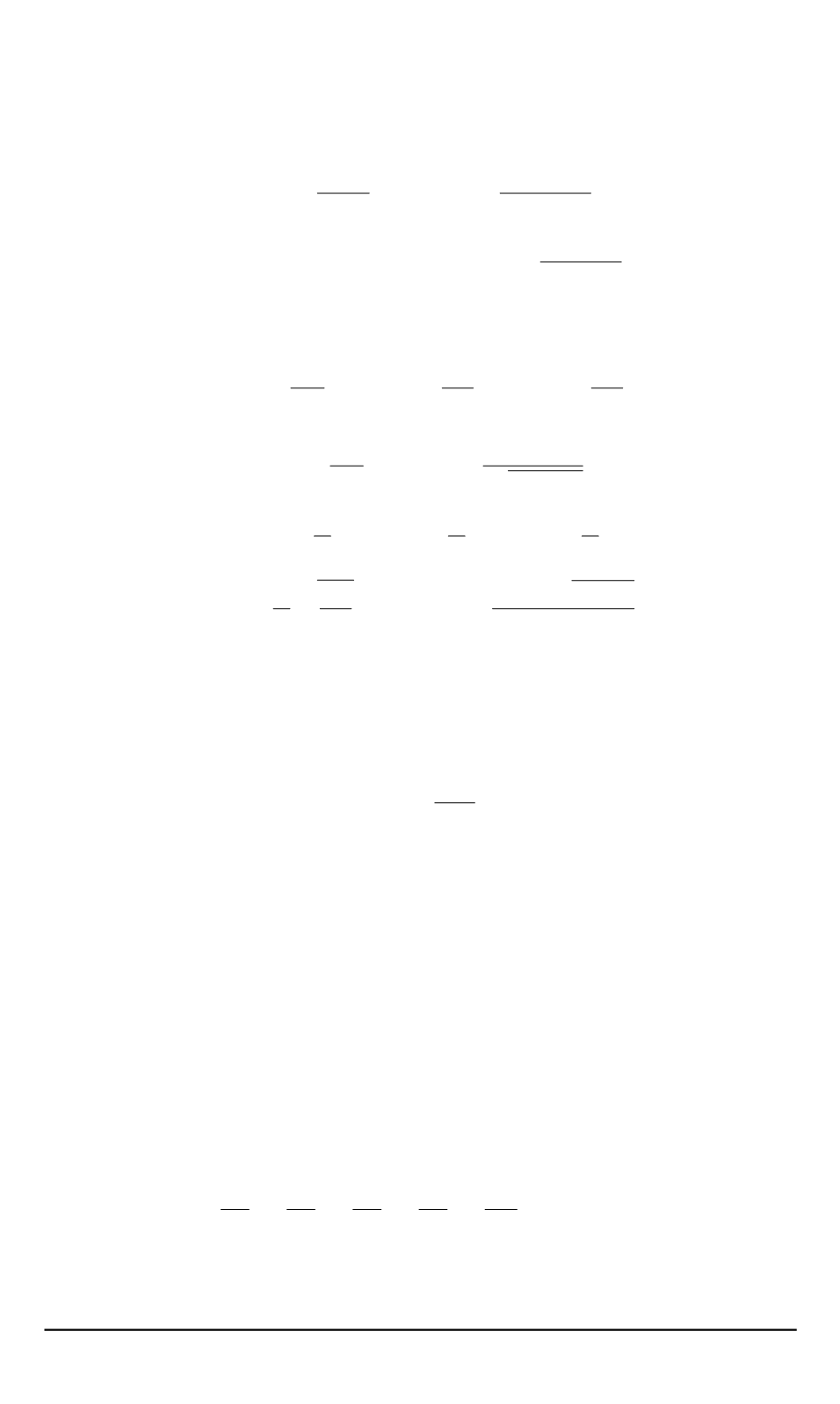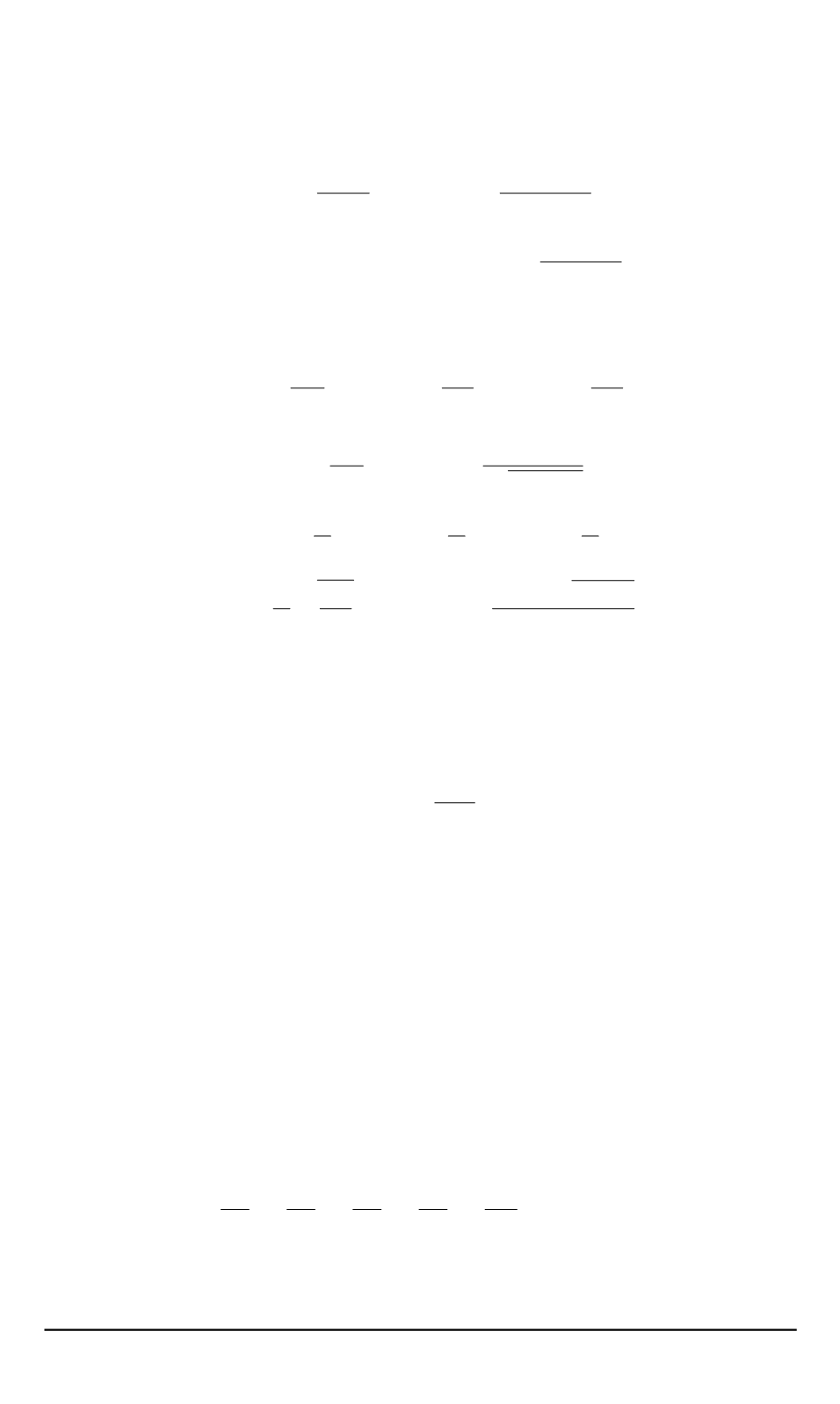
[
ρ
∞
] =
г/см
3
,
k
i
— константы скоростей обратных реакций,
K
i
—
константы равновесия.
Константы, используемые в функциях
ϕ
ij
, имеют следующие раз-
мерности:
[
K
i
] =
h
моль
см
3
i
,
[
k
i
] =
h
см
6
моль
2
∙
с
i
,
[
K
j
]
— безразмерные
,
[
k
j
] =
h
см
3
моль
∙
с
i
,
где
i
= 1
,
2
,
3
,
j
= 4
,
5
,
6
.
Вводятся следующие безразмерные величины:
μ
безр
=
μ
μ
∞
, p
безр
=
p
p
∞
, ρ
безр
=
ρ
ρ
∞
,
T
безр
=
T
T
∞
, ~V
безр
=
~V
p
p
∞
/ρ
∞
,
x
безр
=
x
L
, y
безр
=
y
L
, z
безр
=
z
L
,
t
безр
=
t
L
r
p
∞
ρ
∞
,
˙
W
i
безр
=
˙
W
i
m
i
√
p
∞
ρ
∞
L
,
где
L
— характерный линейный размер.
Дополняют систему уравнений сведения о константах равновесия
и скоростях химических реакций [1, 5] (см. табл. 4) и безразмерное
уравнение состояния, которое принимает вид
p
=
ρT
m
∞
m
.
Сформулируем основные положения, при которых исследуется
рассматриваемая задача:
1) набегающий на затупленное тело поток газа — сверхзвуковой,
однородный и невозмущенный (
γ
= 1
,
4)
;
2) течение во всей возмущенной телом области — ламинарное и
симметричное относительно плоскости, проходящей через ось сим-
метрии тела;
3) уравнения Навье–Стокса справедливы для описания течения во
всей возмущенной телом области;
4) из вязкостных эффектов учитывается динамическая вязкость
μ
.
Условия симметричности течения имеют следующий вид:
∂u
∂x
=
∂v
∂x
=
∂ρ
∂x
=
∂p
∂x
=
∂T
∂x
=
w
= 0
,
где
u
,
v
,
w
— компоненты вектора скорости
~V
, переменная
x
соответ-
ствует координатной линии, перпендикулярной плоскости симметрии.
82
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 1