Равновесное значение расстояния между ядрами
R
0
= 1
,
50
(дан-
ные представлены в атомной системе единиц). Рассчитав равновес-
ное состояние, т.е. получив значение вариационного параметра, можно
усовершенствовать двухчастичную функцию плотности:
n
2
(
~r
1
, ~r
2
) = ˜
Ce
−
γ
2
(
μ
1
+
μ
2
)
α
1
+
α
2
ν
2
1
+
ν
2
2
−
2
α
3
ν
1
ν
2
,
(2)
где
α
1
,
α
2
,
α
3
— вариационные параметры.
Функция (2) также неотрицательна и обладает симметрией отно-
сительно перестановок:
n
2
(
~r
1
, ~r
2
) =
n
2
(
~r
2
, ~r
1
)
.
Параметры функции плотности
α
1
,
α
2
,
α
3
и связанные с ними
характеристики системы могут быть определены вариационными ме-
тодами по аналогии с предыдущим вычислением.
Равновесные значения параметров для пробной двухчастичной
функции плотности приведены в таблице.
Таблица
Параметры пробной двухчастичной функции плотности
α
1
α
2
α
3
R
0
E
0
T
[
n
2
]
V
[
n
2
]
W
[
n
2
]
2,237 0,805 0,273 1,552 – 1,106 0,979 – 2,285 0,201
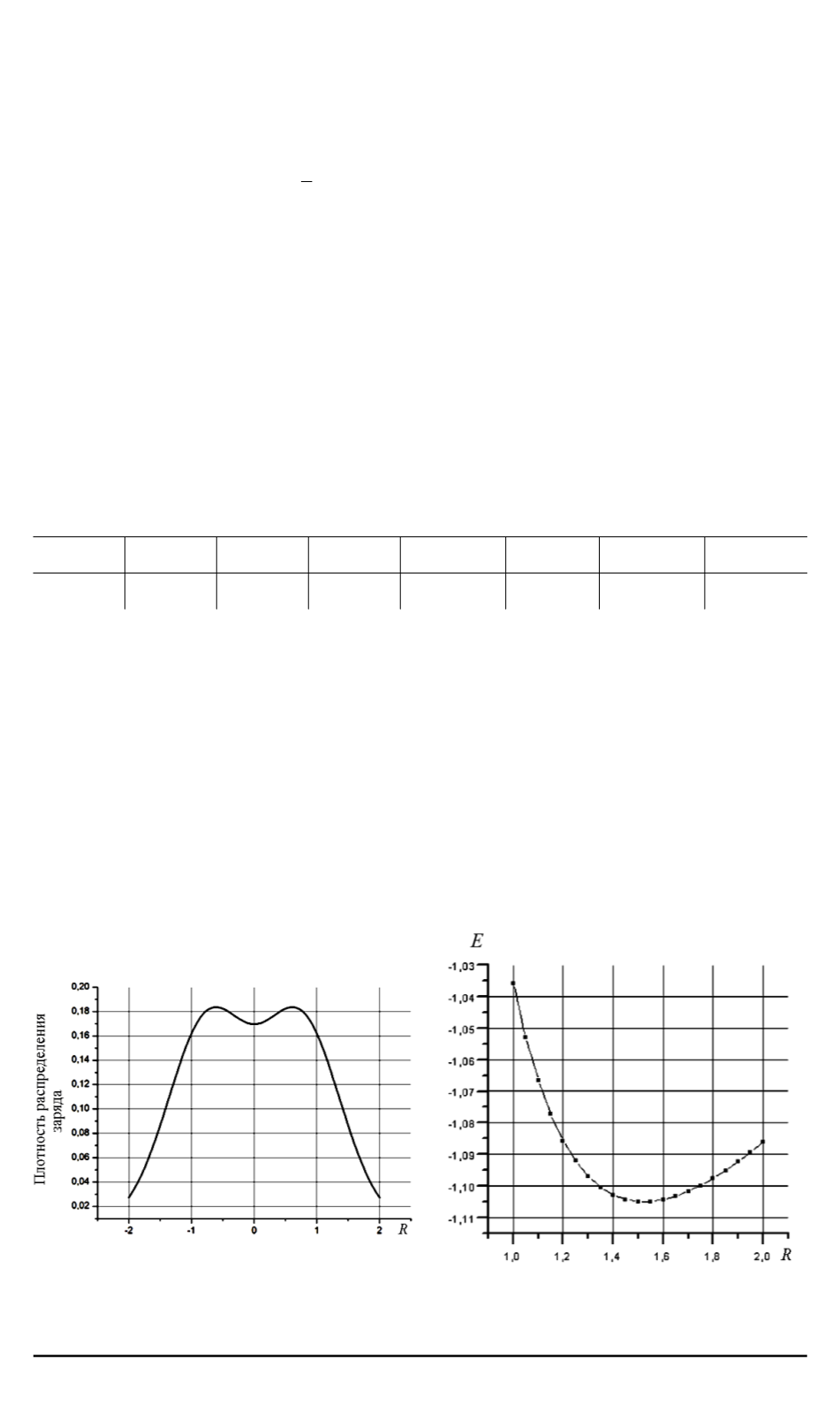
Распределение электронной плотности вдоль прямой, соединяю-
щей ядра атомов, приведено на рис. 1.
Для данной структуры получено: равновесное расстояние между
атомами
r
= 1
,
5
, энергия ионизации
E
= 0
,
165
(результаты расчетов
представлены в атомной системе единиц).
Зависимость полной энергии системы от межъядерного расстояния
приведена на рис. 2.
Учет кинетической энергии ядер дает поправку первого порядка
в адиабатическом приближении. Для ее нахождения воспользуемся
Рис. 1.
Распределение электронной
плотности вдоль прямой, соединяющей
ядра атомов
Рис. 2. Зависимость полной энергии
от межъядерного расстояния
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
37


