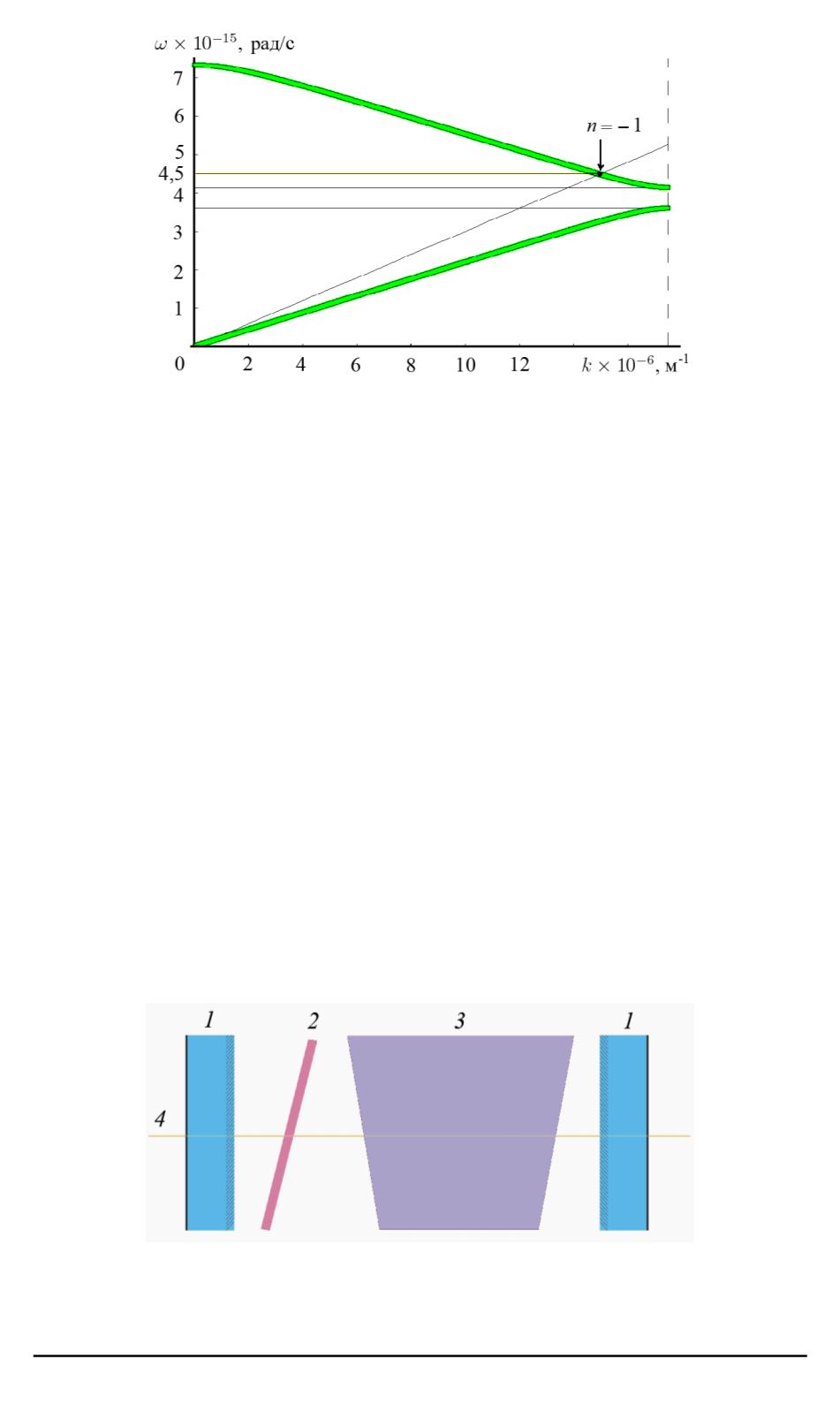
Рис. 2. Дисперсионные кривые фотонного кристалла
n
2
=
n
2
(
ω, ϕ
)
. Соответственно, при заданном угле падения
ϕ
условие
отсутствия отражения
R
= 0
и равенство
n
2
(
ω, ϕ
) =
−
n
1
будут вы-
полняться только для определенной частоты
ω
. При изменении угла
падения
ϕ
условие отсутствия отражения будет реализовано для дру-
гого значения частоты. Используя это свойство, можно создать се-
лективный фильтр на основе фотонного кристалла. Поворачивая его
на определенный угол к падающему лучу света, можно выделять из
спектра волну определенной частоты, для которой излучение будет
проходить через фильтр без потерь на отражение. На рис. 3 приведена
схема использования такого рода фильтра в лазерном резонаторе для
селекции различных линий генерации активной среды.
Выводы.
Получены формулы для расчета коэффициентов отраже-
ния при падении волны на поверхность раздела “правой” и “левой”
сред. Для случая вещественных показателей преломления приведены
обобщенные формулы Френеля, применимые для расчета коэффици-
ентов отражения на границе раздела как двух “правых”, так и “правой”
и “левой” сред. Предсказанный эффект полной прозрачности среды,
Рис. 3. Схема устройства лазера:
1
— оптический резонатор;
2
— селективный фильтр с отрицательным коэффициен-
том преломления;
3
— активная среда и система накачки;
4
— лазерный луч
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
53


