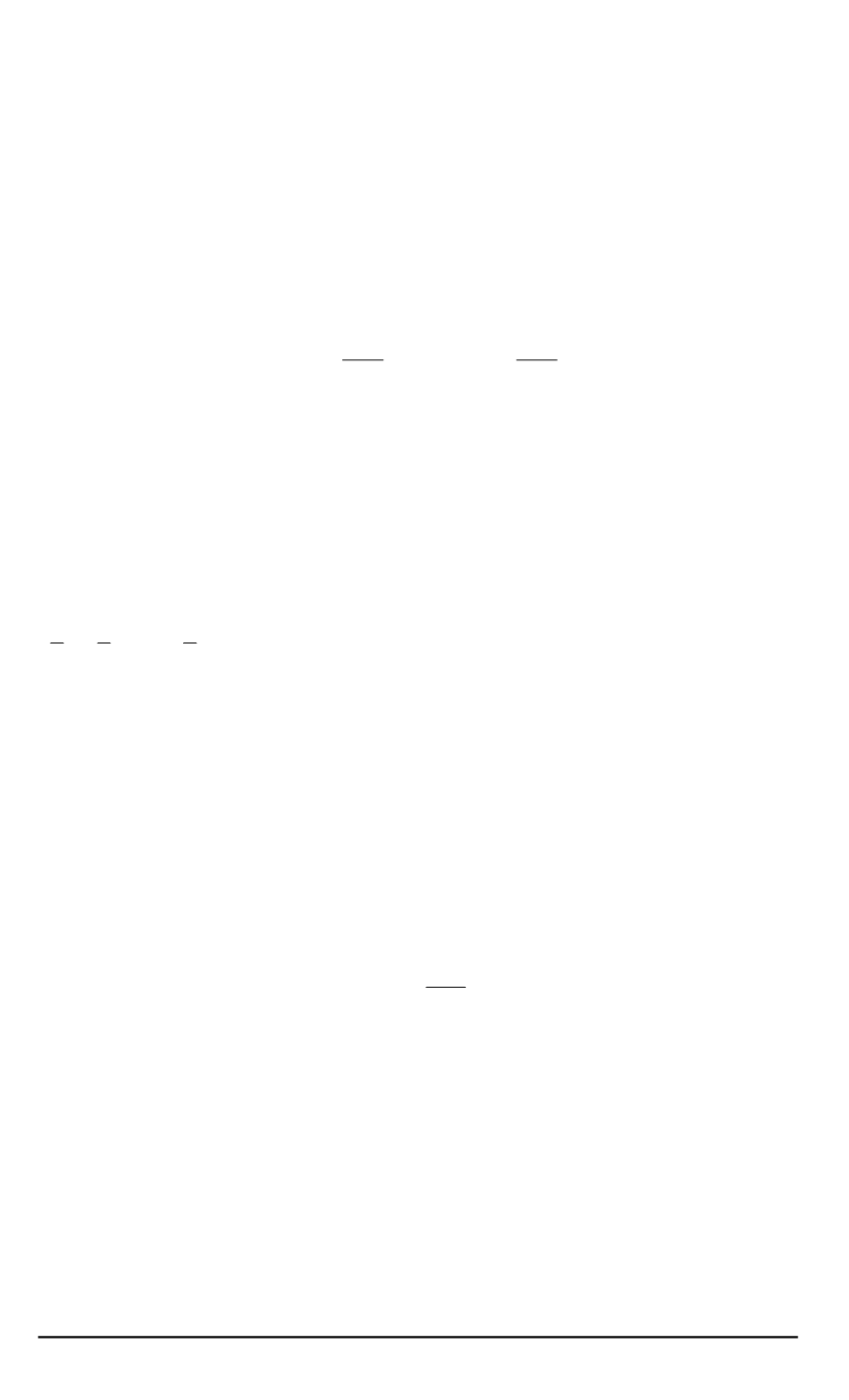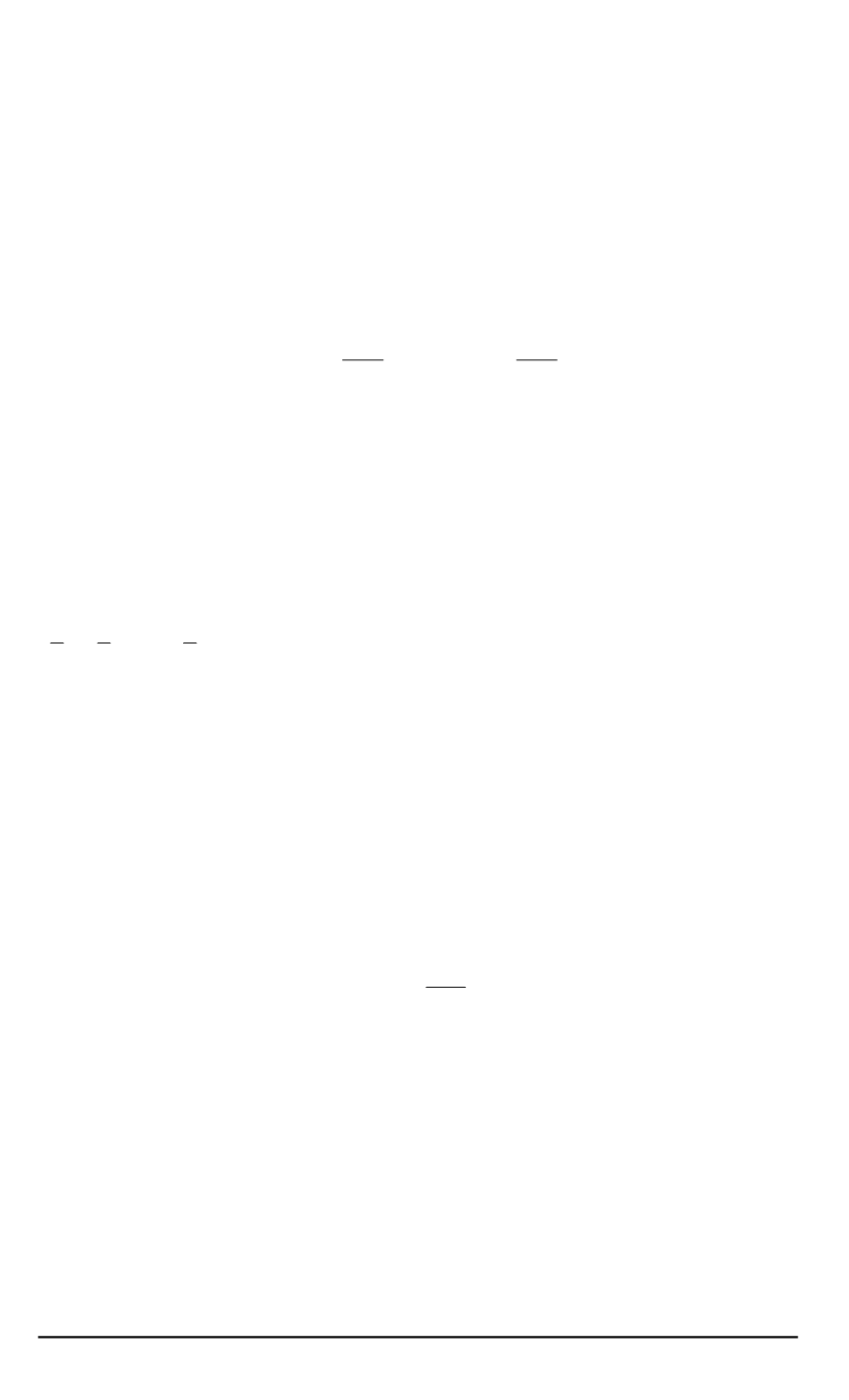
Поскольку левая часть уравнения
(8)
при
Λ
k
(
x
)
>
0,
C
k
(
x
)
>
0
явля
-
ется самосопряженным положительно определенным дифференциаль
-
ным оператором
[5],
то матрица бесконечной системы
(13)
симметри
-
ческая и положительно определенная
.
Преобразуем бесконечную систему
(13)
к следующему виду
:
δ
n
b
(
k
)
n
+
∞
∑
m
=
0
m
6
=
n
B
(
k
)
nm
δ
m
b
(
k
)
m
=
S
(
k
)
n
,
n
=
0
,
1
,
2
, ...
;
(14)
здесь
B
(
k
)
nm
=
C
(
k
)
nm
C
(
k
)
nn
,
S
(
k
)
n
=
g
(
k
)
n
C
(
k
)
nn
.
В этом случае
[6]
для коэффициентов
B
(
k
)
nm
и свободных членов
S
(
k
)
n
справедливы оценки
∞
∑
n
,
m
=
0
|
B
(
k
)
nm
|
2
<
∞
,
∞
∑
n
=
0
|
S
(
k
)
n
|
2
<
∞
.
(15)
Условия
(15)
позволяют применить для решения бесконечной систе
-
мы
(14)
метод редукции
(6),
т
.
е
.
приближенное решение
{
b
(
k
)
0
,
b
(
k
)
1
, . . . ,
b
(
k
)
N
−
1
,
0
,
0
, ...
}
,
сходящееся по норме в
`
2
к точному ре
-
шению
{
b
(
k
)
0
,
b
(
k
)
1
, ...,
b
(
k
)
N
−
1
,
b
(
k
)
N
, ...
}
,
можно найти из конечной системы
N
-
го порядка
δ
n
¯
b
(
k
)
n
+
N
−
1
∑
m
=
0
B
(
k
)
nm
δ
m
¯
b
(
k
)
m
=
S
(
k
)
n
,
n
=
0
,
1
, ...,
N
−
1
.
(16)
Таким образом
,
приближенное аналитическое решение исходной зада
-
чи
(1)–(4)
в каждый момент времени
t
=
t
k
находится в форме тригоно
-
метрического полинома
u
(
r
,
t
k
)
≈
N
−
1
∑
n
=
0
δ
n
¯
b
n
cos
n
π
r
R
,
0
<
r
<
R
,
где коэффициенты
¯
b
(
k
)
n
определяются из решения линейной системы
(16).
В силу того
,
что
C
(
k
)
nm
—
симметрическая положительно опреде
-
ленная матрица
,
то решение конечной системы
N
-
го порядка
(16)
может
быть получено методом Зейделя
[7].
Число уравнений в системе
(16)
выбирается на основе оценки Рун
-
ге
.
Путем решения систем при
N
=
N
1
и
N
=
N
2
,
N
1
<
N
2
,
проверяется
выполнение неравенства
max
r
|
u
(
k
)
N
1
−
u
(
k
)
N
2
|
<
δ
.
ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2003.
№
2 25