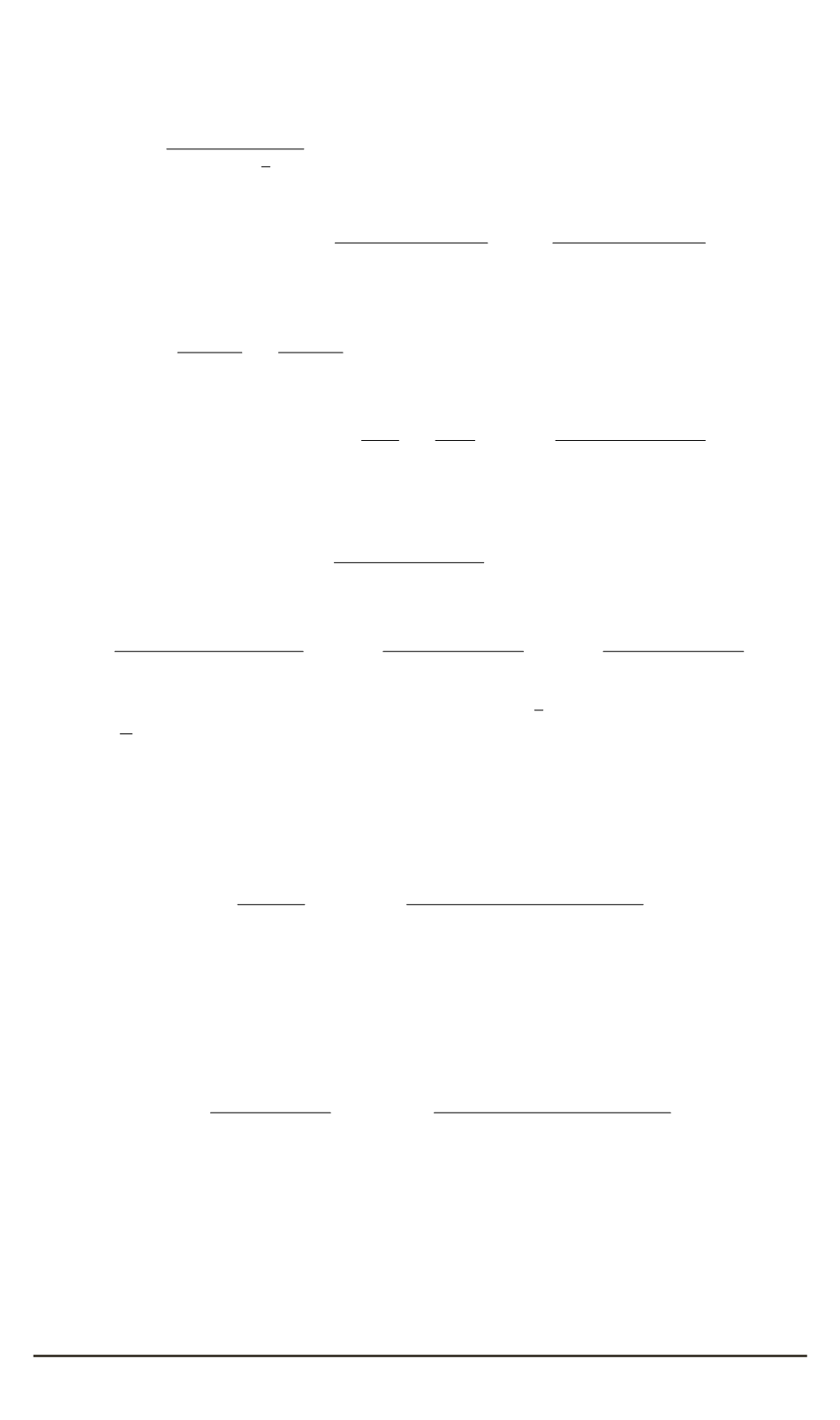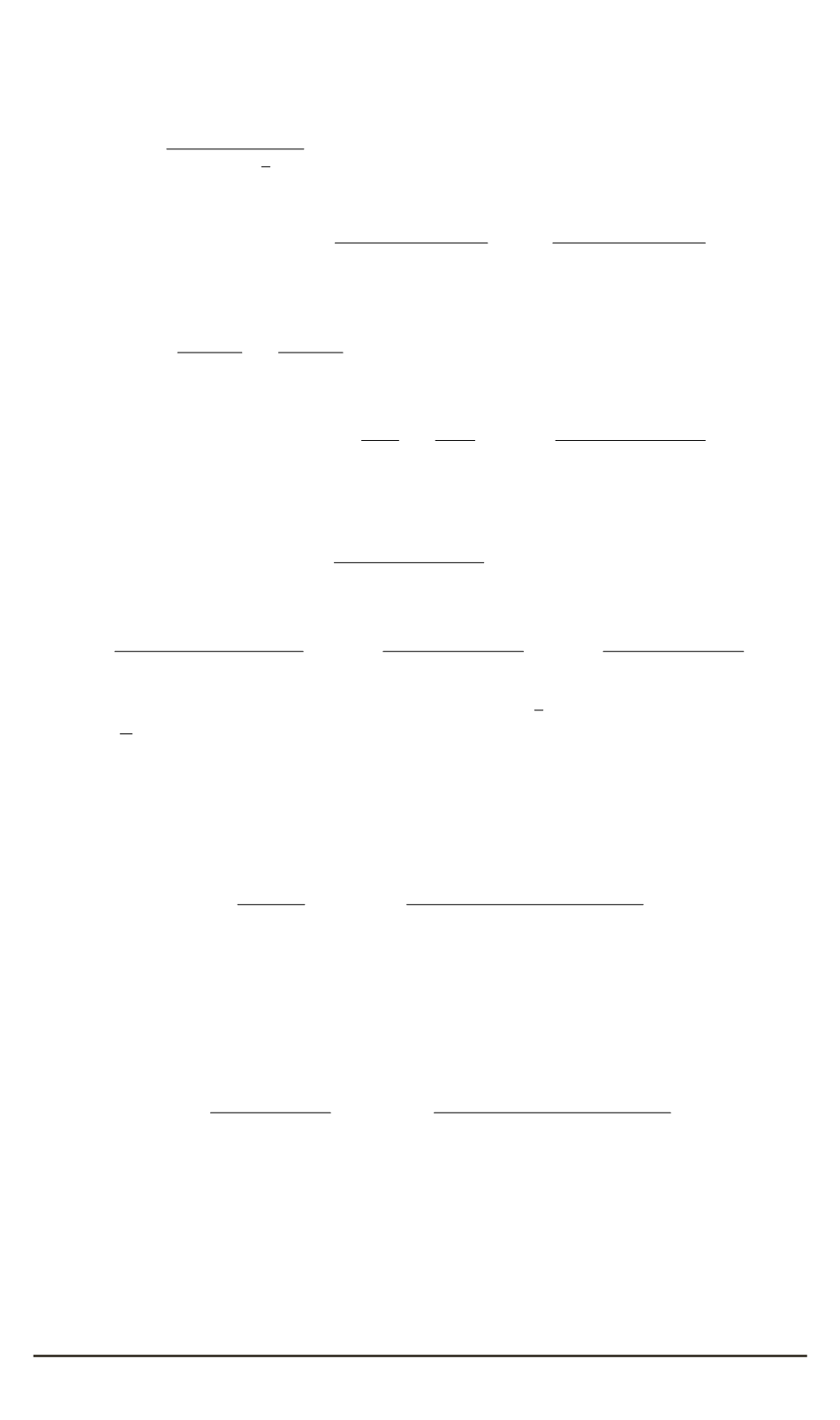
Потребуем, чтобы каждый интеграл был меньше
ε/
3
. После преобра-
зований получаем
I
2
=
y
−
ε
Z
y
0
+
ε
0
ε
+
ψ
+
(
y
)
ψ
+
ε
(
y
)
dy
≤
≤
y
−
ε
Z
y
0
+
ε
0
ε
+
m
+
(
m
+
−
ε
+
)
dy <
ε
+
(
y
−
y
0
)
m
+
(
m
+
−
ε
+
)
< ε/
3;
I
1
≤
y
0
+
ε
0
Z
y
0
1
ψ
−
(
y
)
−
1
ψ
+
(
y
)
dy
≤
≤
y
0
+
ε
0
Z
y
0
1
m
−
−
1
M
+
dy
=
ε
0
(
M
+
−
m
−
)
m
−
M
+
< ε/
3
.
Аналогично
I
3
≤
ε
(
M
+
−
m
−
)
m
−
M
+
< ε/
3
.
Следовательно, если
ε
+
<
εm
+
2
3(
y
−
y
0
) +
εm
+
;
ε
0
<
εm
−
M
+
3(
M
+
−
m
−
)
;
ε <
εm
−
M
+
3(
M
+
−
m
−
)
(10)
и выполнены неравенства (9), то функция
ψ
+
ε
(
y
)
удовлетворяет усло-
вию
t
+
(
ε
)
< t
inf
+
ε
.
I
Для построения аппроксимации функции
ψ
−
(
y
)
обозначим
λ
3
(
y
) =
ξ
(
τ, ξ
−
)
,
где
τ
=
y
−
y
0
ε
0
;
ξ
−
=
ψ
0
−
ψ
+
(
y
0
)
ψ
−
(
y
0
)
−
ψ
+
(
y
0
) +
ε
−
.
Аналогично
λ
4
(
y
) =
η
(
ν, η
−
)
,
где
ν
=
y
−
y
+
ε
ε
;
η
−
=
ψ
−
ψ
+
(
y
)
ψ
−
(
y
)
−
ψ
+
(
y
) +
ε
−
.
В качестве аппроксимации функции
ψ
−
(
y
)
запишем
ψ
−
ˆ
ε
(
y
)=
(
ψ
−
(
y
) +
ε
−
)
λ
3
(
y
) +
ψ
+
(
y
)(1
−
λ
3
(
y
))
, y
2
[
y
0
, y
0
+
ε
0
];
ψ
−
(
y
) +
ε
−
,
y
2
[
y
0
+
ε
0
, y
−
ε
];
(
ψ
−
(
y
) +
ε
−
)
λ
4
(
y
) +
ψ
+
(
y
)(1
−
λ
4
(
y
))
, y
2
[
y
−
ε , y
]
,
где
ˆ
ε
= (
ε
−
, ε
0
, ε
)
.
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3