значений параметров
ω
0
и
S
e
в зависимости от числа
Re
, при кото-
рых вращающийся профиль имеет наименьшее лобовое сопротивле-
ние, посвящены многие расчетные работы, например [5–7].
Поскольку при изучении явления стабилизации следа в работе
[4] принималось
ω
0
= 0
,
5
π
2
S
e
= 0
,
5
π
2
n
Sh
, а значение
n
достаточ-
но велико, пиковые значения скорости движения границы профиля
v
|
K
=
ω
0
D/
2
будут примерно на порядок больше скорости набегаю-
щего потока. Поэтому численное моделирование такого эффекта тре-
бует устойчивости схемы при высоком значении местного числа
Re
.
Впервые численно эффект Танеды был воспроизведен в работе [8],
в которой использовался бессеточный метод вязких вихревых доме-
нов. Сведений о моделировании этого явления сеточными методами
обнаружить не удалось.
Следовательно, численное моделирование обтекания кругового
профиля, совершающего вращательные колебания при различных
значениях
ω
0
и
S
e
, является не только актуальной практической зада-
чей, возникающей, например, при расчете нагрузок, действующих на
элементы конструкций ветроэнергетической установки [2], но и хоро-
шим тестом для верификации методов вычислительной аэрогидроди-
намики.
Постановка задачи.
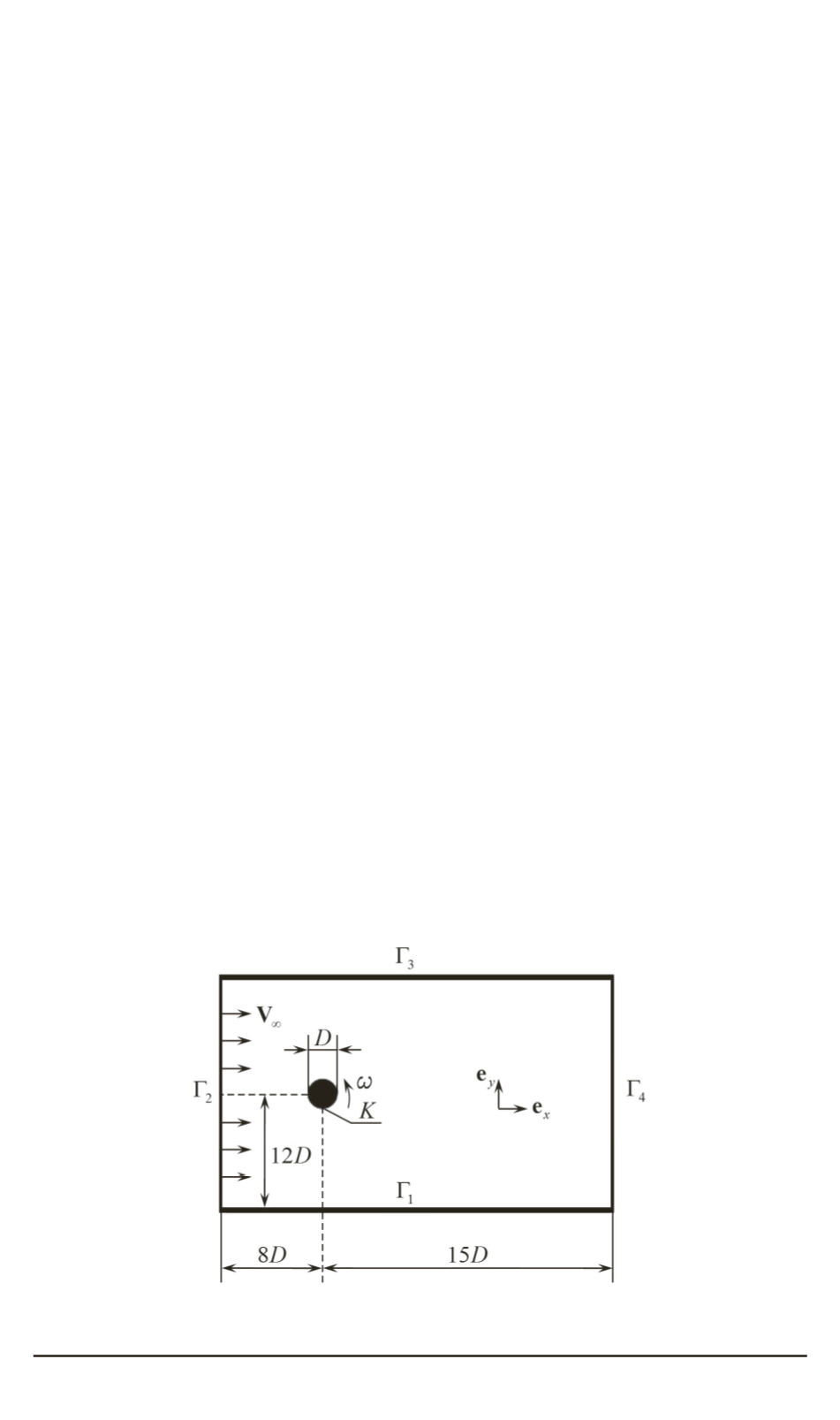
Рассмотрим внешнее обтекание кругового
профиля с границей
K
и диаметром
ˉ
D
, совершающего вращательные
колебания, равномерным потоком вязкой несжимаемой среды посто-
янной плотностью
ˉ
ρ
в расчетной области
Ω = [0
,
23 ˉ
D
]
×
[0
,
24 ˉ
D
]
(рис. 1) с внешней границей
Γ = Γ
1
∪
Γ
2
∪
Γ
3
∪
Γ
4
.
Математическая постановка задачи в безразмерных переменных
имеет вид
Рис. 1. Схема расчетной области
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3
95


