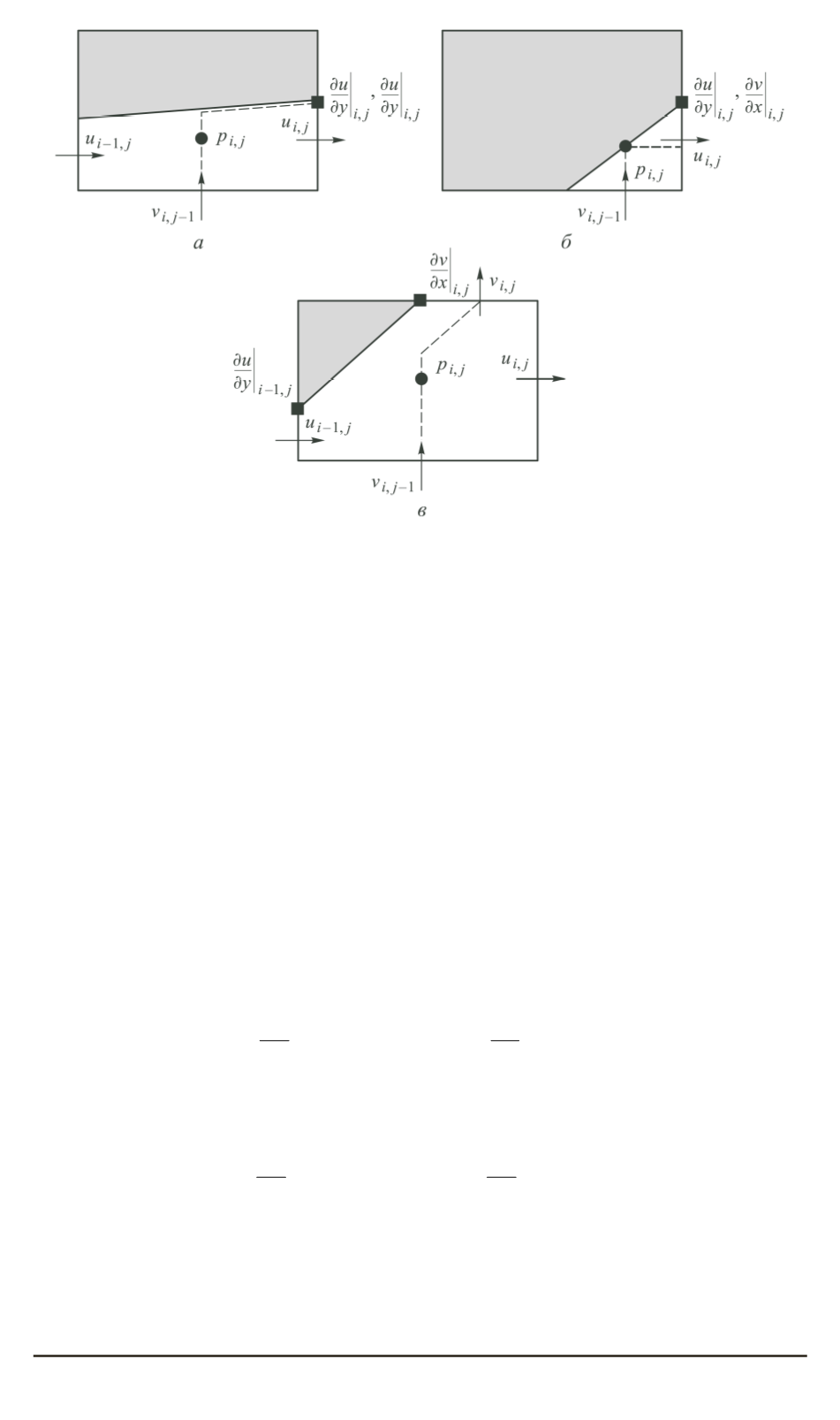
Рис. 2. Примеры усеченных ячеек:
а
— северная трапеция;
б
— северо-западный треугольник;
в
— северо-западный
пятиугольник
Неизвестные значения скоростей
u
i,j
и
v
i,j
вычисляются в точ-
ках, находящихся в серединах жидких частей граней, которые явля-
ются центрами контрольных объемов
Ω
u
i,j
= (
x
c
i
, x
c
i
+1
)
×
(
y
j
−
1
, y
j
)
и
Ω
v
i,j
= (
x
i
−
1
, x
i
)
×
(
y
c
j
, y
c
j
+1
)
с границами
Γ
u
i,j
и
Γ
v
i,j
соответственно.
Точка вычисления давления
p
i,j
(см. рис. 2) расположена на пересече-
нии линий, содержащих точки вычисления скоростей. Это выполнено
исключительно для наглядности и не используется при дискретизации
уравнений: давление аппроксимируется кусочно-постоянной функци-
ей на каждой усеченной ячейке. Такой подход приводит к равенству
нулю градиента давления на твердых стенках. Для сохранения пяти-
точечной структуры шаблона также необходимо по-разному аппрок-
симировать потоки нормальных напряжений
Z
Γ
u
i,j
∂u
∂x
e
x
∙
n dS,
Z
Γ
v
i,j
∂v
∂y
e
y
∙
n dS
и касательных напряжений
Z
Γ
u
i,j
∂u
∂y
e
y
∙
n dS,
Z
Γ
v
i,j
∂v
∂x
e
x
∙
n dS.
В жидких и усеченных ячейках с одной твердой гранью нормальные
напряжения рассчитываются в центре ячейки
Ω
i,j
, а касательные —
в правом верхнем углу. Для остальных усеченных ячеек положения
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3
97


