
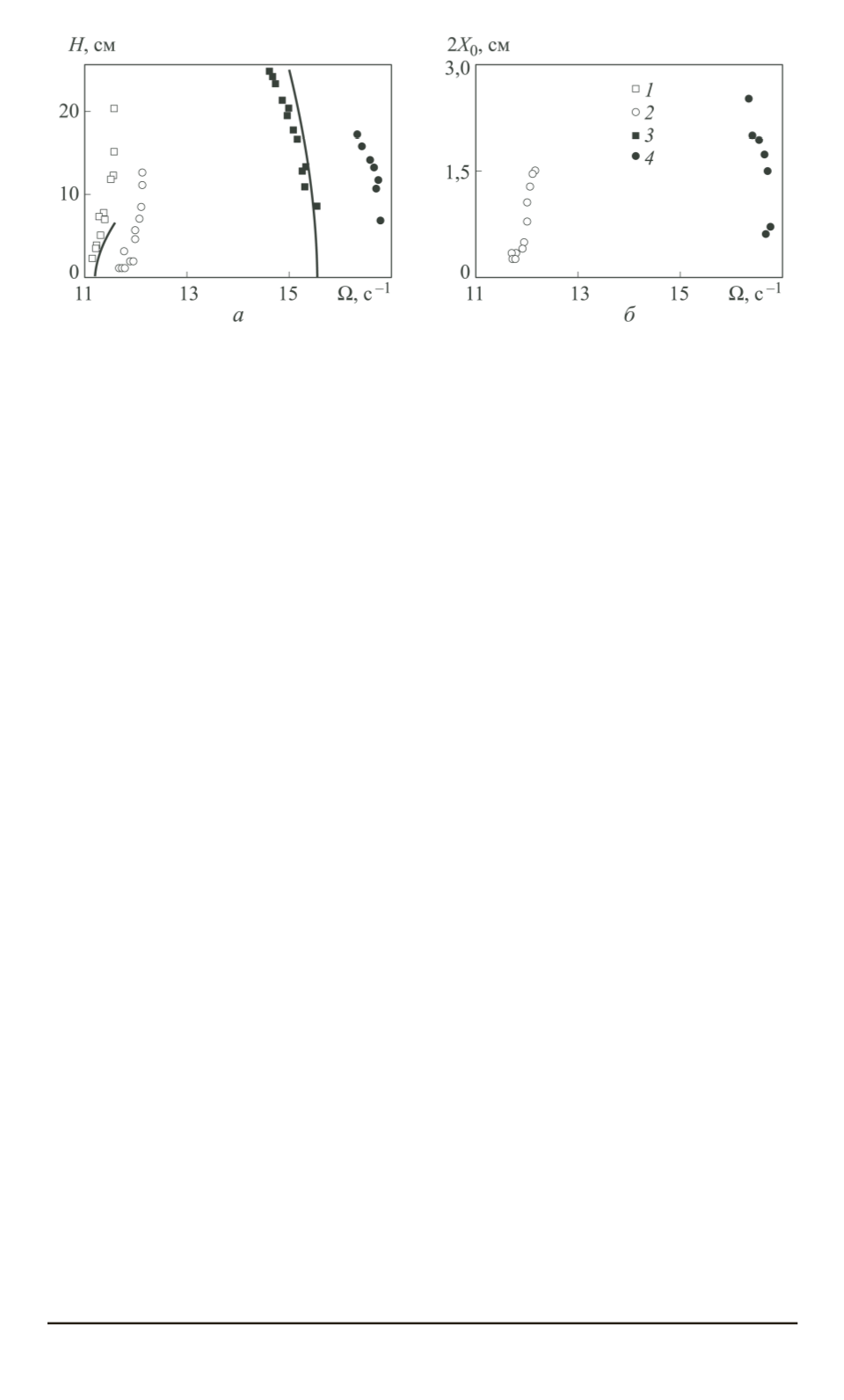
Рис. 2. Резонансная зависимость
H
(Ω)
первой волновой моды (
а
) и зависимость
размаха
2
X
0
колебаний тележки от частоты
Ω
(
б
) для неподвижного в
горизонтальном направлении сосуда,
h
= 10
, 20 см (
1
,
3
), сосуда на тележке,
h
= 10
, 20 см (
2
,
4
), устойчивая ветвь (
5
), рассчитанная по (1), модель [17]
увеличением частоты колебаний сосуда (кривая
1
). При
h
= 20
см
величина
β
= 0
,
060
положительна, наклон резонансной зависимости
изменяется (кривая
3
) и реализуется параметрическое возбуждение
с мягкой восстанавливающей силой. Отметим, что в двух случаях
модель неплохо описывает экспериментальные данные до крутизны
волны
H/λ
≈
0
,
15
, причем отсутствует смещение измеренных и рас-
считанных зависимостей по частоте. Некоторое различие измеренных
и рассчитанных значений высоты
H
связано с нелинейностью наблю-
даемых в эксперименте волн, для которых узла стоячей волны как
неподвижной точки свободной поверхности не существует. Профили,
приведенные на рис. 3, соответствуют двум режимам стационарных
колебаний свободной поверхности жидкости, построенным при нало-
жении 8 и 9 видеокадров (отвечают полупериоду волны) при частоте
вертикальных колебаний сосуда
Ω = 11
,
26
и
11
,
53
с
−
1
. Если в пер-
вом случае (рис. 3,
а
) волна имеет крутизну
H/λ
≈
0
,
04
и близка
к линейной, то при
H/λ
≈
0
,
22
(рис. 3,
б
) в значительной степени
проявляются нелинейные эффекты: интенсивные колебания узла сто-
ячей волны, асимметрия профиля и отрывы небольших фрагментов
жидкости.
Волны Фарадея в подвижном сосуде
.
Рассмотрим случай по-
движного в горизонтальном направлении сосуда с жидкостью:
ϕ
1
6
= 0
,
ϕ
2
6
= 0
.
Оценим воздействие колеблющейся жидкости на сосуд. При от-
сутствии волн гидростатическое давление на торцевые стенки сосуда
дает горизонтальную нулевую силу. При наличии на поверхности во-
ды свободных стоячих двумерных волн амплитуда силы, действующей
в горизонтальном направлении, оценивается в первом приближении
по интегралу Коши – Лагранжа как
Q
X
=
HL
2
Wρω
2
/π
2
. Например,
18
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1

















