
образом, при анализе связанных колебаний системы сосуд – жидкость
вместо линейной волновой частоты
ω
=
q
gk
th
kh
следует использо-
вать частоту
ω
∗
, зависящую от глубины или массы жидкости.
Оценка частотного сдвига
.
Проведем анализ экспериментальных
данных, используя результаты Л.Н. Сретенского о плоских горизон-
тальных колебаниях прямоугольного сосуда с идеальной жидкостью
при наличии на поверхности свободной стоячей волны [10]. Указанная
задача соответствует случаю
ϕ
1
= 0
, ϕ
2
6
= 0
.
Движение сосуда с жидкостью на тележке (см. рис. 1) описывается
уравнением
m
¨
X
=
Q
x
, где
m
=
m
1
+
m
2
;
m
1
=
ρLWh
и
ρ
— масса и
плотность жидкости;
m
2
— масса сосуда на тележке.
Полагая, что горизонтальные колебания системы происходят с ча-
стотой
ω
∗
и амплитудой
X
0
, а сила
Q
X
в линейном приближении
определяется как
Q
X
=
∞
X
n
=1
,
3
,...
ρ
16
L
2
WX
0
ω
∗
4
(
−
1)
n
−
1
2
n
3
π
3
(
gk
n
thk
n
h
−
ω
∗
2
)
th
k
n
h
+ 2
LWhX
0
ω
∗
2
!
cos
ω
∗
t,
получаем следующее уравнение для частоты
ω
∗
:
−
M
+ 1
Mω
∗
2
=
∞
X
n
=1
,
3
,...
8
L
n
3
π
3
h
(
gk
n
−
ω
∗
2
ch
k
n
h
)
,
(2)
где
M
=
m
1
/m
.
Представив левую и правую части (2) функциями
F
1
(
ω
∗
2
)
и
F
2
(
ω
∗
2
)
,
найдем графически решение этого уравнения. Для первой волновой
моды при глубине жидкости 20 см частота связанных колебаний опре-
деляется пересечением кривых
1
и
2
, приведенных на рис. 5,
а
. Частота
ω
∗
2
смещена вправо относительно собственной частоты первой волно-
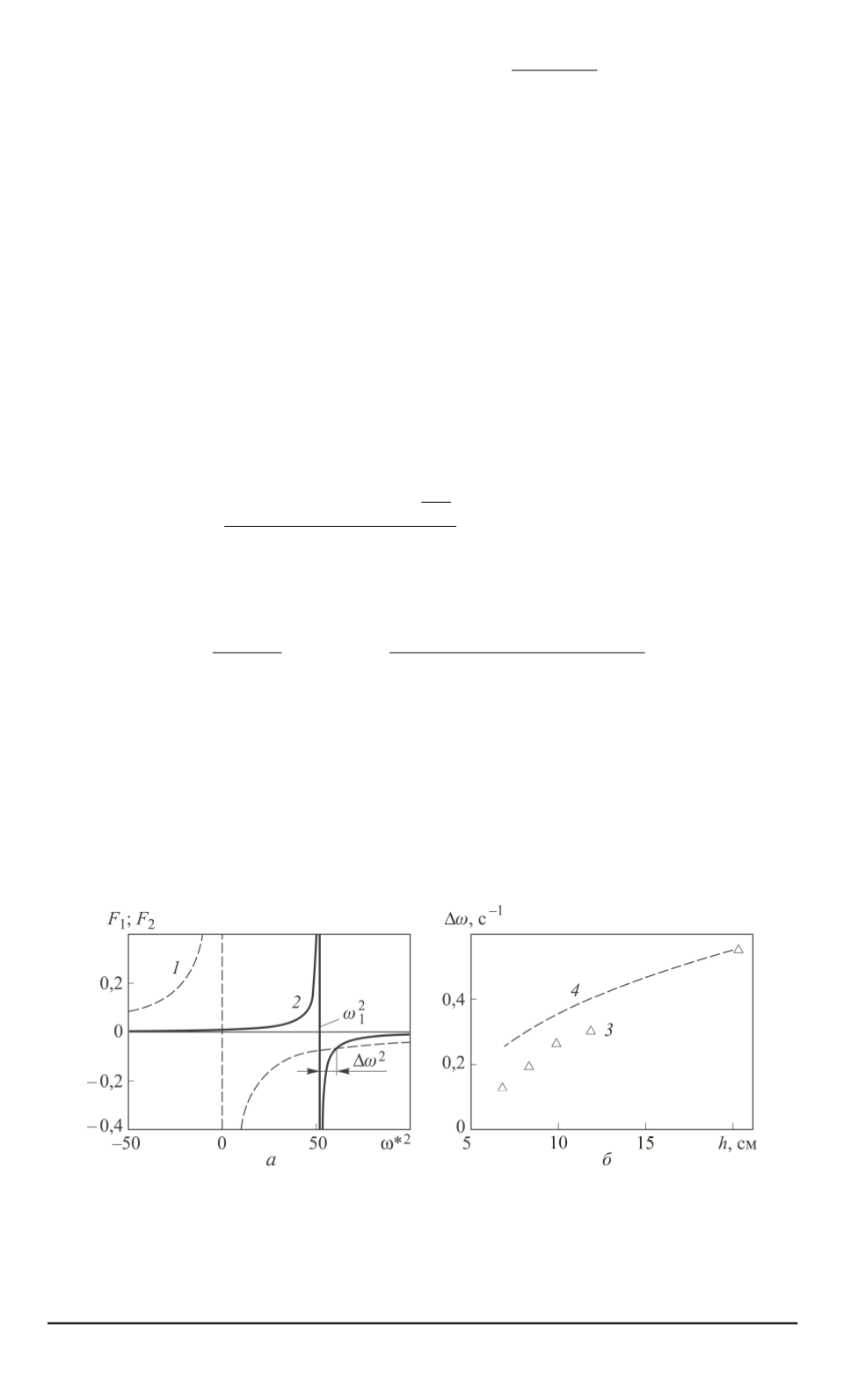
Рис. 5. Графическое решение уравнения (2) и оценка частотного сдвига
Δ
ω
по точке пересечения кривых функций
F
1
(
1
) и
F
2
(
2
) для первой моды
стоячих волн на свободной поверхности жидкости глубиной
h
= 20
см (
а
),
экспериментальная (
3
) и расчетная (
4
) зависимости частотного сдвига от
глубины жидкости (
б
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1
21

















