
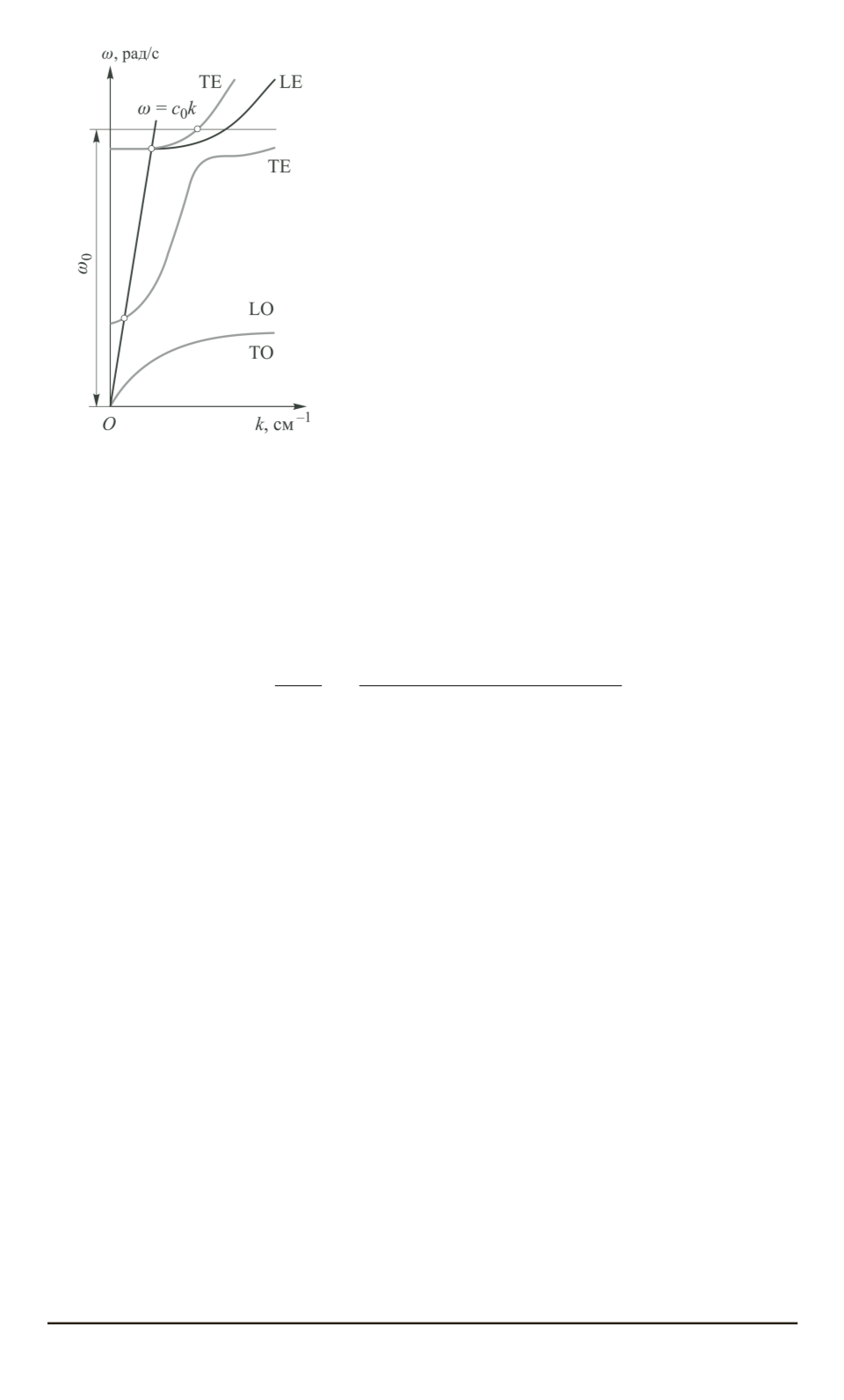
Рис. 2. Схематический вид по-
ляритонных кривых в реше-
точной и экситонной областях
спектра
излучения, позволяет вычислить часто-
ты поляритонов нижней ветви и по-
строить участок дисперсионной кривой
поляритонов в этом кристалле. Таким
образом, методом КР в нецентросимме-
тричных кристаллах может быть реали-
зована конверсия фотонов в поперечные
и продольные решеточные возбуждения
материальных сред. В случае спонтанно-
го КР коэффициент преобразования при
такой конверсии очень мал и составляет
приблизительно
10
−
6
.
В экситонной области спектра в
диэлектрических и полупроводниковых
кристаллах формируются так называ-
емые светоэкситоны, или поперечные
и продольные экситонные поляритоны
(TE, LE). В простейшей модели учет как решеточных, так и экси-
тонных поляритонов приводит к закону дисперсии для поперечных
волн в виде
ω
2
=
c
2
0
k
2
ε
(
ω
)
=
c
2
0
k
2
(
ω
2
01
−
ω
2
)(
ω
2
02
−
ω
2
)
(
ω
2
l
1
−
ω
2
)(
ω
2
l
2
−
ω
2
)
.
Схематически закон дисперсии решеточных и экситонных поля-
ритонов проиллюстрирован на рис. 2. С учетом эффекта простран-
ственной дисперсии параметры в (2) зависят от волнового вектора,
т.е. имеют вид функций
ω
01
=
ω
01
(
k
);
ω
02
=
ω
02
(
k
);
ω
l
1
=
ω
l
1
(
k
);
ω
l
2
=
ω
l
2
(
k
)
.
Отметим, что на поляритонных кривых (см. рис. 2) присутствуют
особые точки, соответствующие так называемым унитарным поля-
ритонам, для которых имеет место
ω
=
с
0
k
, т.е. соответствующий
показатель преломления
n
= 1
.
Наряду с полярными (векторными) бозонами в материальных сре-
дах присутствуют скалярные бозоны, соответствующие полносимме-
тричным (“дыхательным”) модам. Согласно правилам отбора, КР на
скалярных бозонах оказывается разрешенным для многих молекуляр-
ных структур как в нецентросимметричных, так и в центросимметрич-
ных средах. Скалярные бозоны соответствуют полносимметричным
осцилляциям атомов (ионов) в молекулах и кристаллах, а также ос-
цилляциям формы микрочастиц, из которых построена материальная
среда. Присутствие этих мод обнаруживается в спектрах неупругого
40
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1

















