
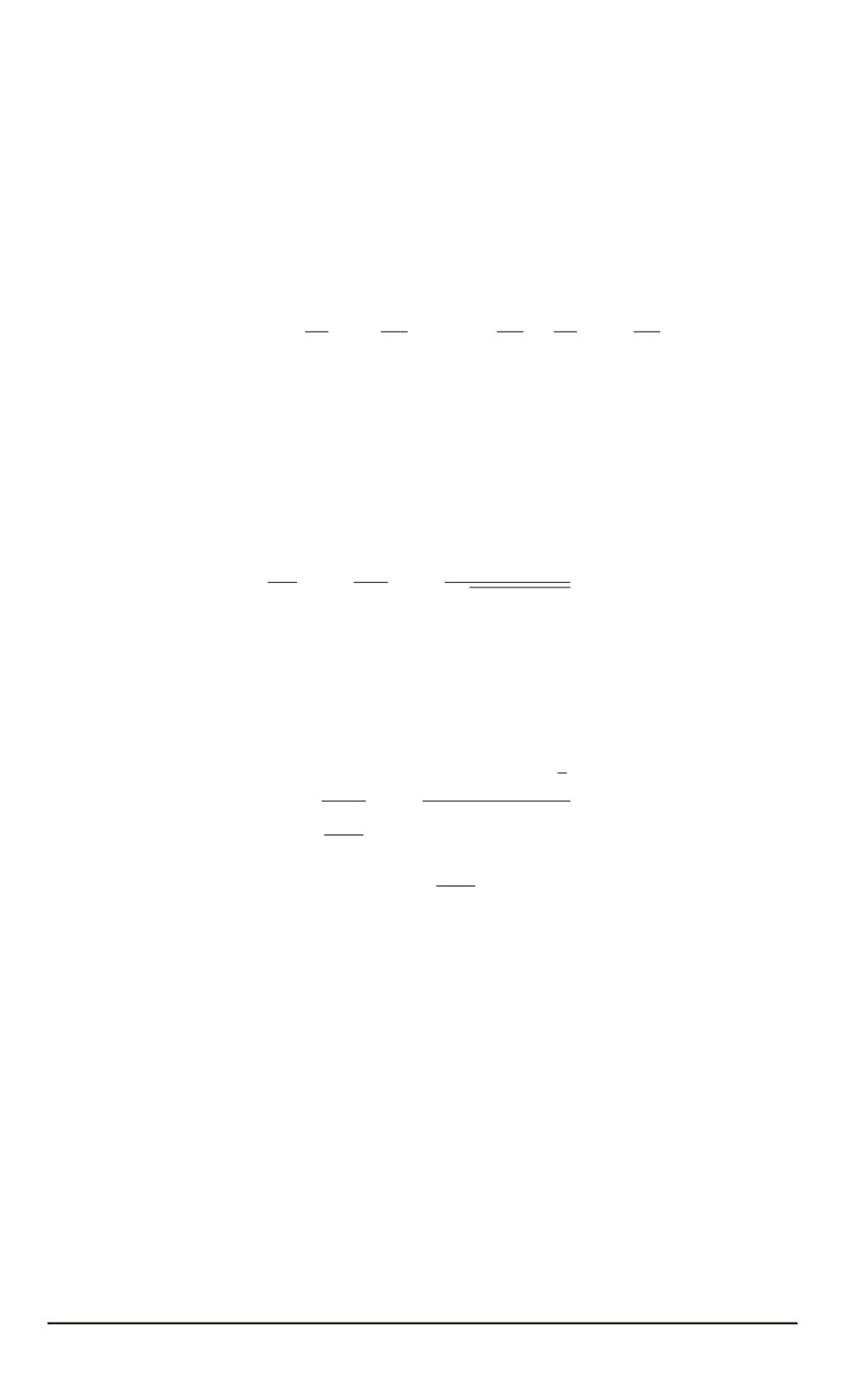
Уравнения движения для трансляционных продольных осцилляций
кластеров в новой (низкотемпературной) фазе принимают вид
M
¨
u
l
(
p
) =
−
γ
0
u
l
(
p
)
−
γ
l
[2
u
l
(
p
)
−
u
l
(
p
−
1)
−
u
l
(
p
+ 1)] ;
p
= 0
,
1
,
2
, . . .
;
γ
l
<
0
, γ
0
>
0
.
Решение уравнений (6) в виде плоских монохроматических волн при-
водит к закону дисперсии для продольных оптических электромагнит-
ных волн (рис. 6,
б
)
ω
2
l
=
ω
2
0
−
4
c
2
a
2
sin
2
ka
2
;
ω
2
0
=
γ
0
M
;
c
2
a
2
=
−
γ
l
M
.
(5)
Соответственно в области малых волновых векторов (приближение
континуума) закон дисперсии (7) удовлетворяет соотношению
ω
2
l
=
ω
2
0
−
c
2
k
2
.
(6)
Групповая скорость волн, соответствующих закону дисперсии (8), мо-
жет быть представлена как
dω
dk
=
−
c
2
k
ω
=
−
c
2
k
p
ω
2
0
−
c
2
k
2
.
(7)
Согласно соотношению (9), направления фазовой и групповой скоро-
стей в этом случае взаимно противоположны. Эффективная масса
m
и
масса покоя
m
0
продольных фотонов в соответствии с выражениями
(8) и (9) являются отрицательными:
m
=
~
d
2
ω
dk
2
=
−
~
(
ω
2
0
−
c
2
k
2
)
3
2
c
2
ω
2
;
m
0
=
m
(0) =
−
~
ω
0
c
2
.
Наряду с трансляционными степенями свободы кластеры низкотем-
пературной фазы вакуума имеют дыхательные и аксионные степени
свободы. Таким образом, в вакууме присутствуют, кроме ветвей век-
торных фотонов (см. рис. 6), две дополнительные дисперсионные ве-
тви, соответствующие парафотонам и аксионам. Законы дисперсии для
парафотонов и аксионов имеют релятивистский вид:
ω
2
=
ω
2
par
+
c
2
0
k
2
;
ω
2
=
ω
2
ax
+
c
2
0
k
2
.
Фотон-бозонная конверсия. Генерация парафотонов, аксионов
и продольных фотонов в лаборатории.
Квантовое описание процес-
сов фотон-бозонной конверсии в материальных средах и в физическом
вакууме осуществляется на основе введения в гамильтониан ангар-
44
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1

















