
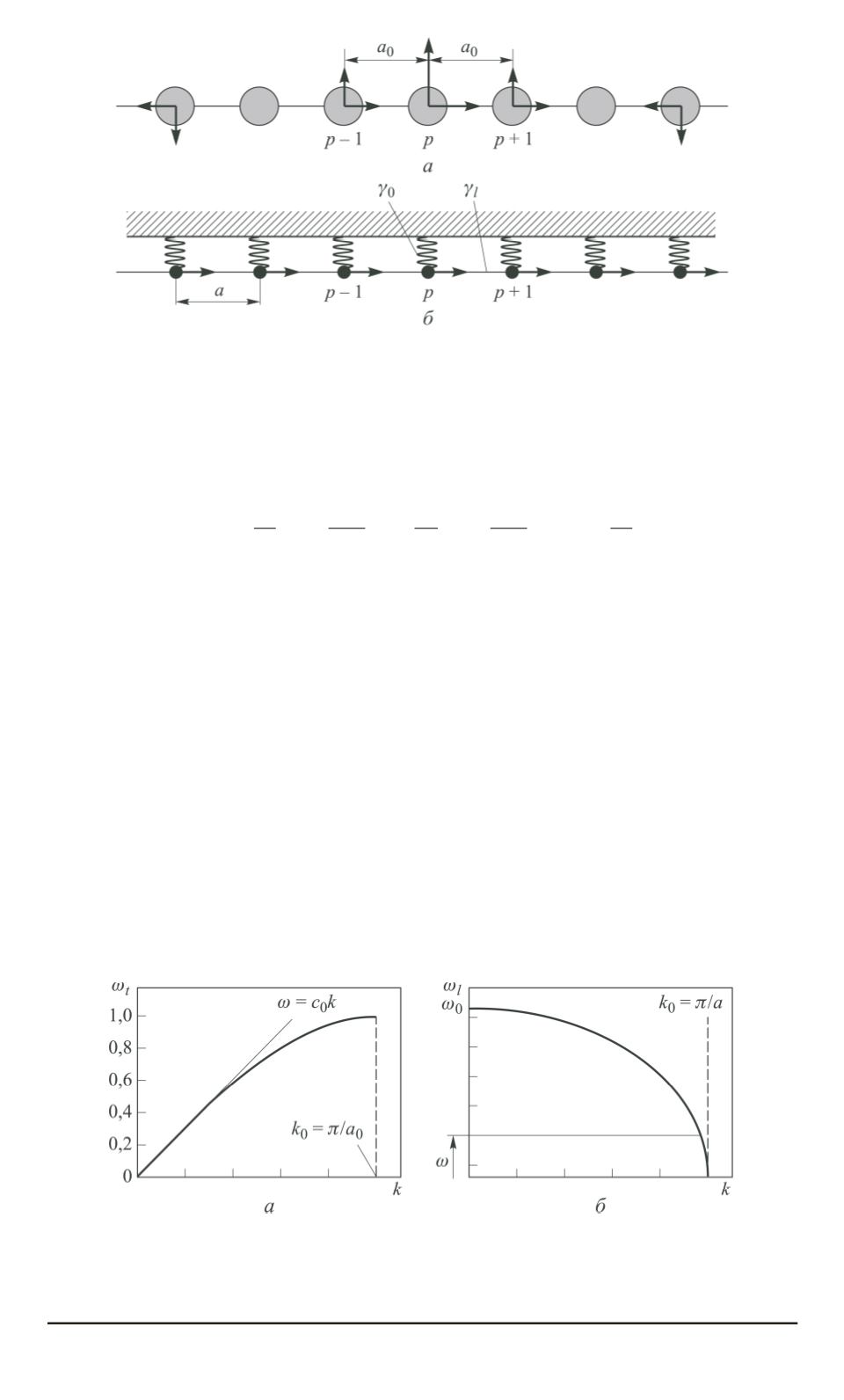
Рис. 5. Модель одномерной гравитационной кристаллической цепочки, не-
устойчивой относительно продольных акустических волн, при
а
0
≈
10
−
33
≈
см
(
а
) и сверхструктура в виде глобулярной гравитационной кристаллической
цепочки при
а
≈
10
−
15
см (
б
)
получаем законы дисперсии соответствующих волн:
ω
2
t
= 4
γ
t
m
sin
2
ka
0
2
= 4
c
2
0
a
2
0
sin
2
ka
0
2
;
c
2
0
=
γ
t
m
a
2
0
;
ω
l
= 0; (
γ
l
= 0)
.
При малых волновых векторах
k
для поперечных акустических
волн физического вакуума закон дисперсии аппроксимируется извест-
ной в теории относительности дисперсионной зависимостью для попе-
речных электромагнитных волн в вакууме:
ω
t
=
с
0
k
, где
с
0
=
с
t
— ско-
рость поперечных электромагнитных волн (скорость света) в вакууме.
Относительно продольных акустических волн исходная фаза физиче-
ского вакуума (прафаза) оказалась неустойчивой (
ω
l
= 0
). В результате
при охлаждении Вселенной произошел структурный фазовый переход
с образованием сверхструктуры c периодом
a a
0
(
а
≈
10
−
15
см,
рис. 5,
б
). Закон дисперсии для поперечных акустических волн в ис-
ходной (высокотемпературной) фазе физического вакуума (прафазе)
приведен на рис. 6,
а
.
Рис. 6. Законы дисперсии для поперечных акустических волн в исходной фазе
вакуума (прафазе) (
а
) и для продольных акустических и оптических волн
вакуума после сверхструктурного фазового перехода (
б
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1
43

















