
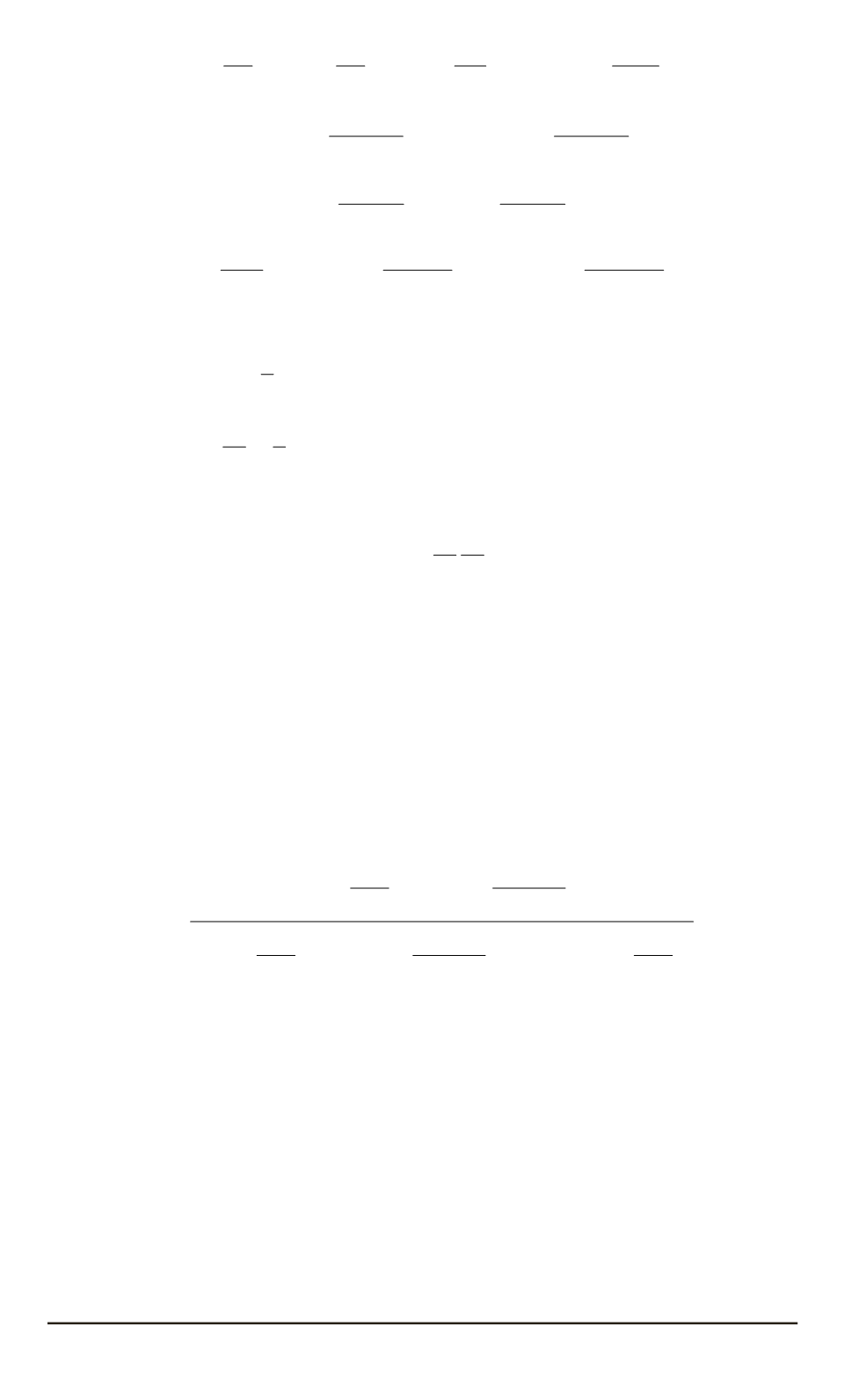
ξ
=
r
R
1
, ξ
1
=
R
2
R
1
,
Fo =
a
1
t
R
2
1
,
Σ(Fo) =
R
(
t
)
R
1
;
e
U
(
ξ,
Fo) =
U
−
T
0
Δ
T
1
,
e
V
(
ξ,
Fo) =
V
−
T
0
Δ
T
2
;
St
1
=
c
1
Δ
T
1
L
,
St
2
=
c
2
Δ
T
2
L
;
e
k
=
kR
1
λ
1
,
e
q
(Fo) =
q
(
t
)
R
1
Δ
T
1
λ
1
,
e
T
1
(Fo) =
T
1
−
T
0
Δ
T
1
.
Исходная задача в безразмерной форме примет вид
e
U
,Fo
=
1
ξ
e
U
,ξ
+
e
U
,ξξ
,
1
< ξ <
Σ(Fo)
,
Fo
>
0;
(26)
e
V
,
Fo
=
a
2
a
1
1
ξ
e
V
,ξ
+
e
V
,ξξ
,
Σ(Fo)
< ξ < ξ
1
,
Fo
>
0;
e
U
(Σ(Fo)
,
Fo) =
e
V
(Σ(Fo)
,
Fo) = 0
,
Fo
>
0;
(27)
Σ
,
Fo
(
Fo
) =
−
St
1
e
U
,ξ
(Σ(Fo)
,
Fo) +
ρ
2
ρ
1
a
2
a
1
St
2
e
V
,ξ
(Σ(Fo)
,
Fo)
,
Fo
>
0;
e
U
(
ξ,
0) = 0
,
e
V
(
ξ,
0) =
−
1
,
Σ(0) = 1;
(28)
−
e
U
,ξ
(1
,
Fo) =
e
k
h e
T
1
(Fo)
−
e
U
(1
,
Fo)
i
+
β
e
q
1
(Fo)
,
e
q
(Fo)
>
0
,
(29)
Fo
>
0
, β
∈
[0; 1];
e
V
,ξ
(
ξ
1
,
Fo) = 0
,
Fo
>
0
.
Пользуясь полученными ранее результатами, найдем решение за-
дачи (26)–(29):
e
U
(
ξ,
Fo) =
E
1
ξ
2
4Fo
−
E
1
Σ
2
(Fo)
4Fo
e
kE
1
1
4Fo
−
e
kE
1
Σ
2
(Fo)
4Fo
+ 2 exp
−
1
4Fo
×
×
h e
k
e
T
1
(Fo) +
β
e
q
1
(Fo)
i
.
(30)
Поскольку краевые условия подзадачи нахождения распределения
температуры в твердой фазе не являются согласованными, нахождение
непрерывного аналитического решения, удовлетворяющего выбран-
ной модели, невозможно. Соответствующие расчеты целесообразно
проводить численно [14].
Полученное соотношение (30) может быть использовано при расче-
тах, связанных с плавлением как в рассмотренных выше накопителях
энергии, так и в накопителях с большим числом тепловых трубок
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1
109

















