
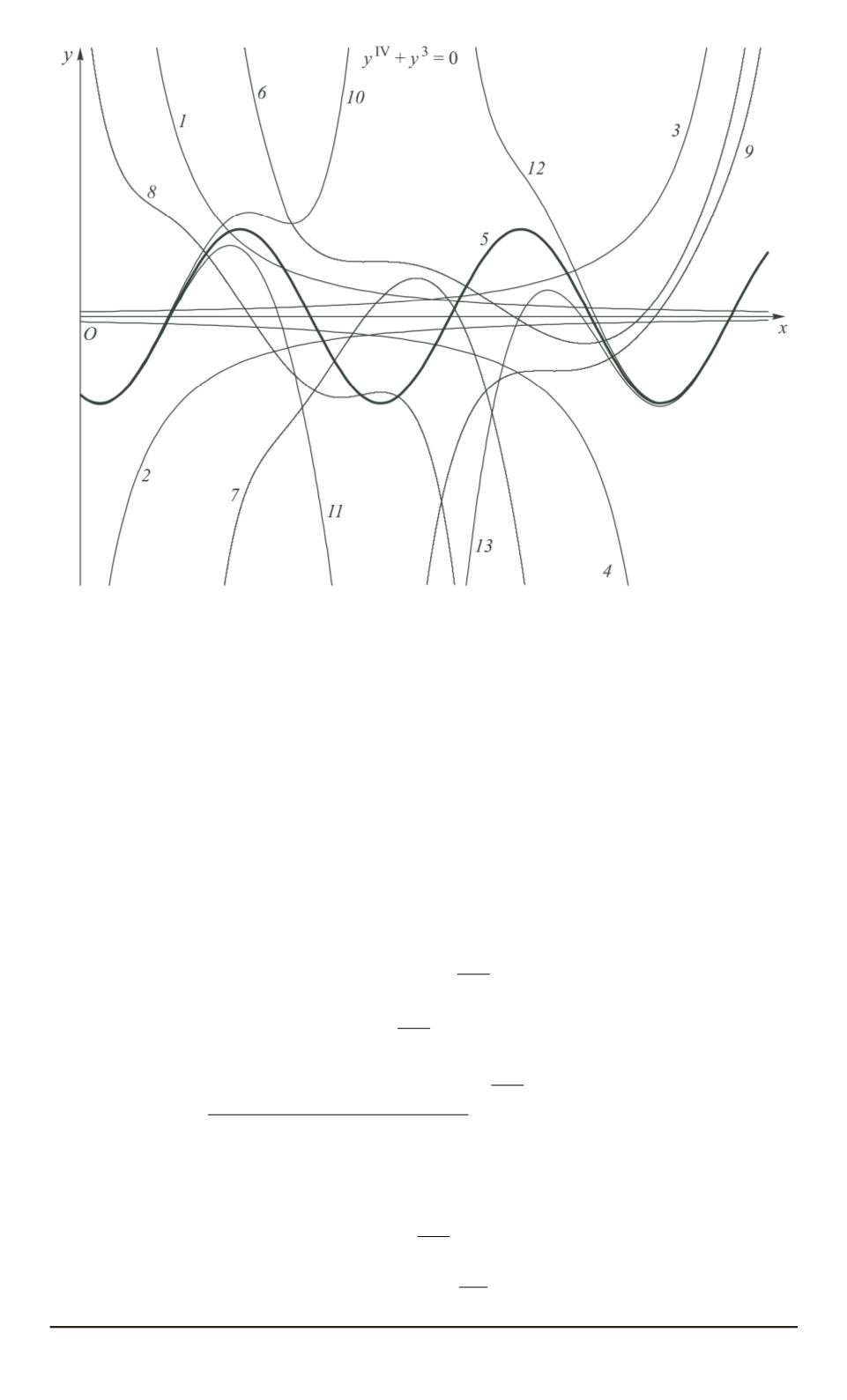
Fig. 4. Solution to equation (2)
Asymptotic Classification of the Solutions to the Fourth-Order
Equation (2).
In this section previously obtained results on the asymptotic
behavior of solutions to equation (2) are formulated [7, 28].
Theorem 3.
Suppose
k >
1
and
p
0
>
0
.
Then all maximally extended
solutions to equation
(2)
are divided into the following fourteen types
according to their asymptotic behavior
(Fig. 4).
0. The trivial solution
y
(
x
)
≡
0
.
1–2. Defined on
(
b,
+
∞
)
Kneser (up to the sign) solutions (see
definition in [5]) with the power asymptotic behavior near the boundaries
of the domain (with the relative signs
±
):
y
(
x
)
∼ ±
C
4
k
(
x
−
b
)
−
4
k
−
1
, x
→
b
+ 0;
y
(
x
)
∼ ±
C
4
k
x
−
4
k
−
1
,
x
→
+
∞
,
where
C
4
k
=
4(
k
+ 3)(2
k
+ 2)(3
k
+ 1)
p
0
(
k
−
1)
4
1
k
−
1
.
3–4. Defined on semi-axes
(
−∞
, b
)
Kneser (up to the sign) solutions
with the power asymptotic behavior near the boundaries of the domain
(with the relative signs
±
):
y
(
x
)
∼ ±
C
4
k
|
x
|
−
4
k
−
1
,
x
→ −∞
;
y
(
x
)
∼ ±
C
4
k
(
b
−
x
)
−
4
k
−
1
, x
→
b
−
0
.
20
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2

















