
Lemma 2.
The sets
Ω
−
∩
S
3
,
Ω
+
∩
S
3
,
Ω
−
∩
E,
and
Ω
+
∩
E
are
homeomorphic to the solid torus.
J
It is sufficient to consider
Ω
+
∩
S
3
.
The set
Ω
+
is the union of its
two homeomorphic subsets
Ω
++
=
+
+
+
+
∪
+
+
+
−
∪
+
+
−
−
∪
+
−
−
−
and
Ω
+
−
=
−
−
−
−
∪
−
−
−
+
∪
−
−
+
+
∪
−
+
+
+
.
In order to describe the set
Ω
++
∩
S
3
,
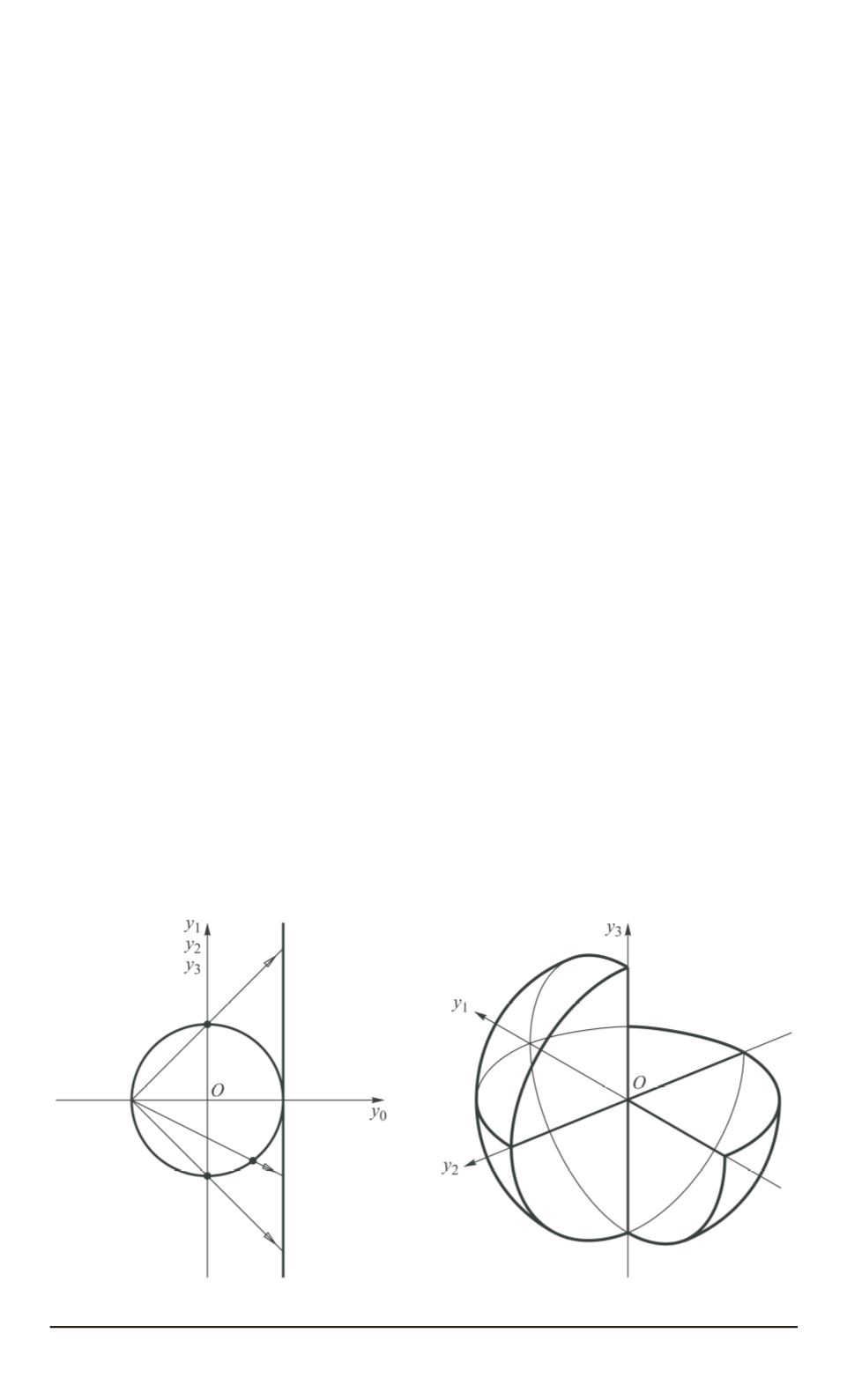
we use the stereographic projection
S
3
\{
(
−
1
,
0
,
0
,
0)
} →
R
3
(Fig. 1).
The image of
Ω
++
∩
S
3
under this projection is contained in the
ball of radius 2 and is equal to the union of its two quarters, which is
homeomorphic to the 3-dimensional ball. The same is true for
Ω
+
−
∩
S
3
.
The intersection
(Ω
++
∩
S
3
)
∩
(Ω
+
−
∩
S
3
) =
0
+
+
+
∪
0
−
−
−
∩
S
3
maps to the disjoint union of two spherical triangles (2-dimensional figures,
Fig. 1. Stereographic projection and its image of
Ω
++
∩
S
3
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2

















