
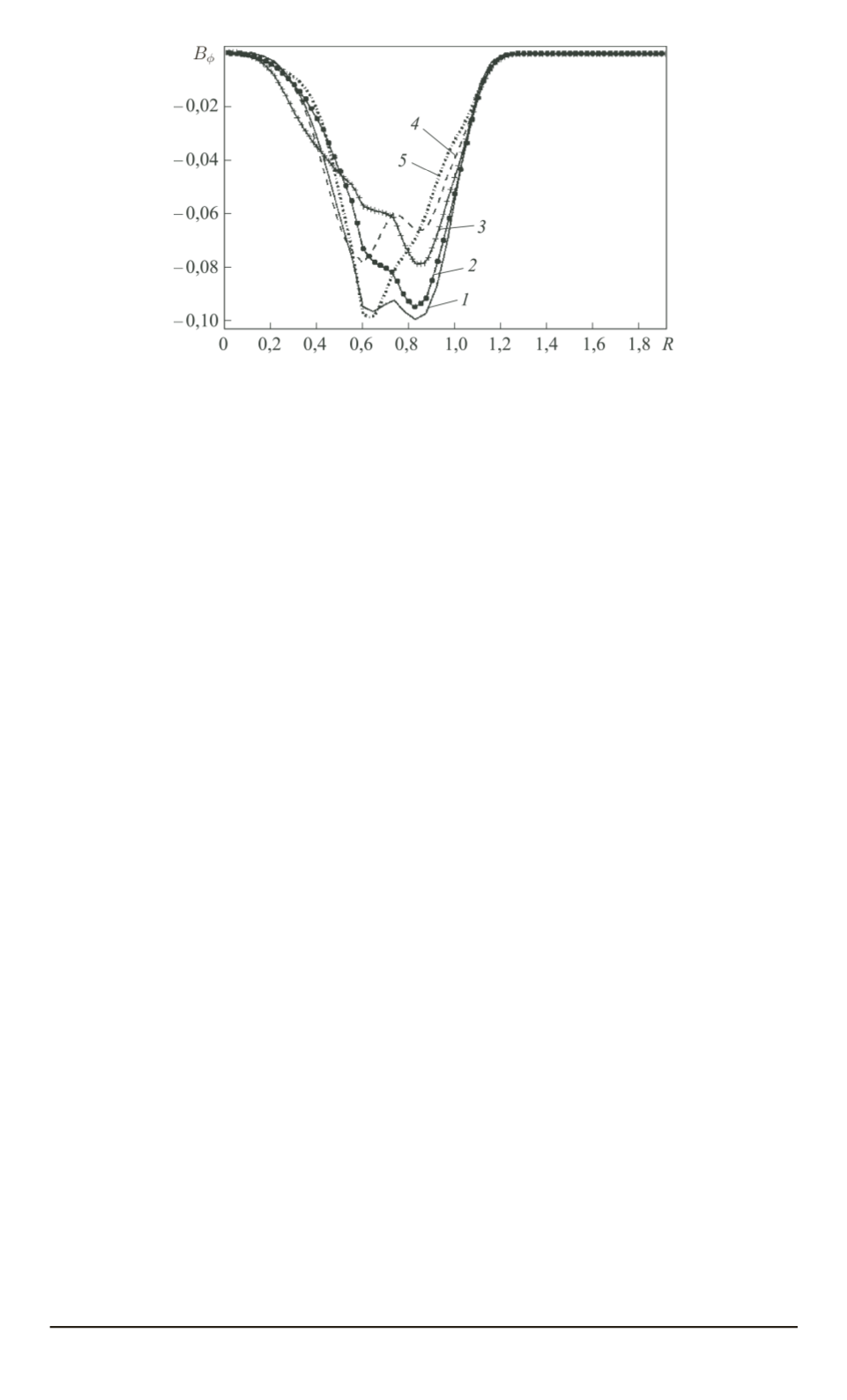
Рис. 11. Угловая компонента магнитного поля вдоль линии
z
= 2
,
5
при
t
= 13
,
95
(
1
), 14,2 (
2
), 14,45 (
3
), 14,7 (
4
) и 14,95 (
5
)
внутреннего джета. С течением времени в поперечном срезе углово-
го магнитного поля образуется новый минимум (этот минимум при-
нимаем за границу внутреннего джета, рис. 11), радиус джета резко
уменьшается, скорость истечения увеличивается. Далее точка мини-
мума начинает смещаться от оси вращения, скорость снижается, пока
не образуется новый минимум (и новая граница внутреннего джета).
Анализ характеристик колебаний позволяет предположить, что они
имеют гравитационное происхождение, причем магнитное поле, сжи-
маемое поперек силовых линий, играет роль пружинки, а вес набега-
ющей незамагниченной плазмы — вынуждающей силы.
Проведенные расчеты показали, что в модели образуется устойчи-
вый во времени канализированный выброс плазмы в положительном
направлении оси
z
. Выброс хорошо коллимирован и по своим параме-
трам хорошо соотносится с имеющимися наблюдательными и расчет-
ными данными о структуре и свойствах галактических джетов. Если
предположить, что частицы плазмы будут светиться в зависимости от
температуры, то для внешнего наблюдателя поток будет выглядеть как
истекающий по спирали джет.
Плотность вещества внутри канала на несколько порядков меньше
плотности вещества стенок, причем сам канал является практически
прозрачным для возможного излучения. Если рассматривать случай
томпсоновского рассеяния излучения на электронах, то оптическая
толщина слоя вещества внутри канала составляет
τ
=
σ
T
nL
0
≈
6
,
7
∙
10
−
4
,
(10)
поэтому для расчета распространения излучения внутри канала при-
менима модель переноса излучения с однократным рассеянием.
Если интерпретировать результаты в размерных величинах, то рас-
четы моделируют истечение от формирующейся протозвезды массой
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
85

















