
Проведены тестовые испытания построенного на основе описанно-
го алгоритма программного комплекса. Рассмотрен ряд стандартных
тестов для численных МГД-кодов:
•
задача о распаде альфвеновской волны (тест численной дисси-
пации разностной схемы);
•
задача о распространении циркулярно поляризованной альфве-
новской волны (тест точности схемы на гладком решении);
•
задача Брио – Ву о распаде разрыва (тест аппроксимации реше-
ния задачи Римана);
•
задача о вращении цилиндра в покоящейся среде (тест устойчи-
вости схемы);
•
задача о вихре Орзага – Танга (тест возникновения ударных волн
и сверхзвуковой турбулентности).
Перечисленные задачи успешно решены, метод показал высокую
устойчивость, умеренный уровень численной диссипации, сверхли-
нейный порядок сходимости решения. Все важные разрывы в реше-
ниях задач передаются физически корректно.
Основные результаты расчетов.
К моменту безразмерного време-
ни
t
= 5
режим течения в расчетной области в целом устанавливает-
ся, головная ударная волна и сопутствующий ей “шлейф” уходят из
области. Система не приходит в стационарный режим, но совершает
колебания относительно некоторого положения равновесия.
Установившийся режим движения системы определяется балансом
полного давления в замагниченной и незамагниченной частях области.
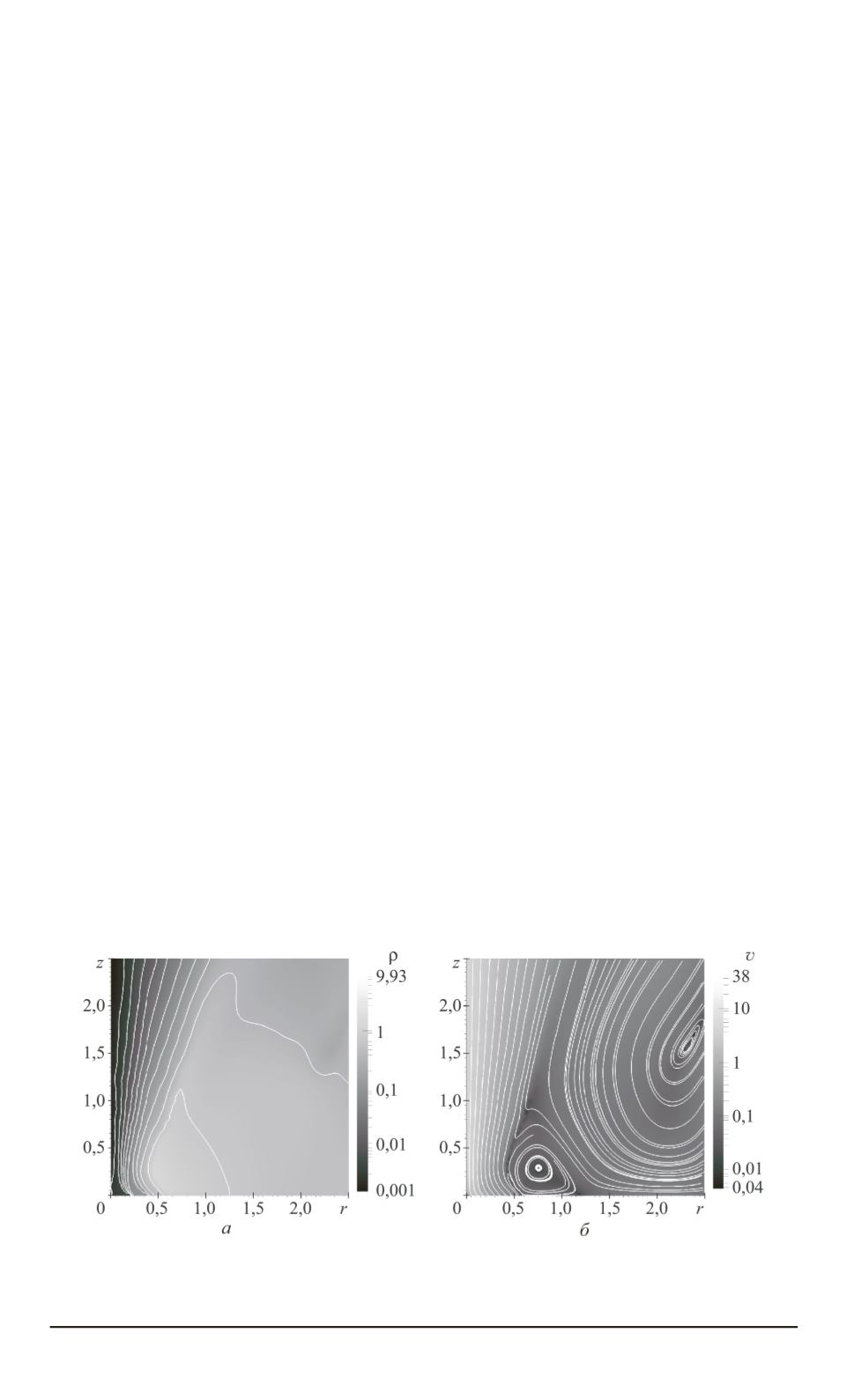
Одна из особенностей режима — образование ускоряющего канала
в замагниченной подобласти
Ω
B
(рис. 8). Течение имеет следующие
характерные черты.
1. Вокруг “горловины” подобласти
Ω
B
— ускоряющего канала —
образуется торовидный фокусирующий вихрь плазмы, скорость дви-
Рис. 8. Распределения плотности (
а
) и скорости (
б
) в момент времени
t
= 15
(установившийся режим выброса) в ускоряющем канале в МГД-модели
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
83

















