
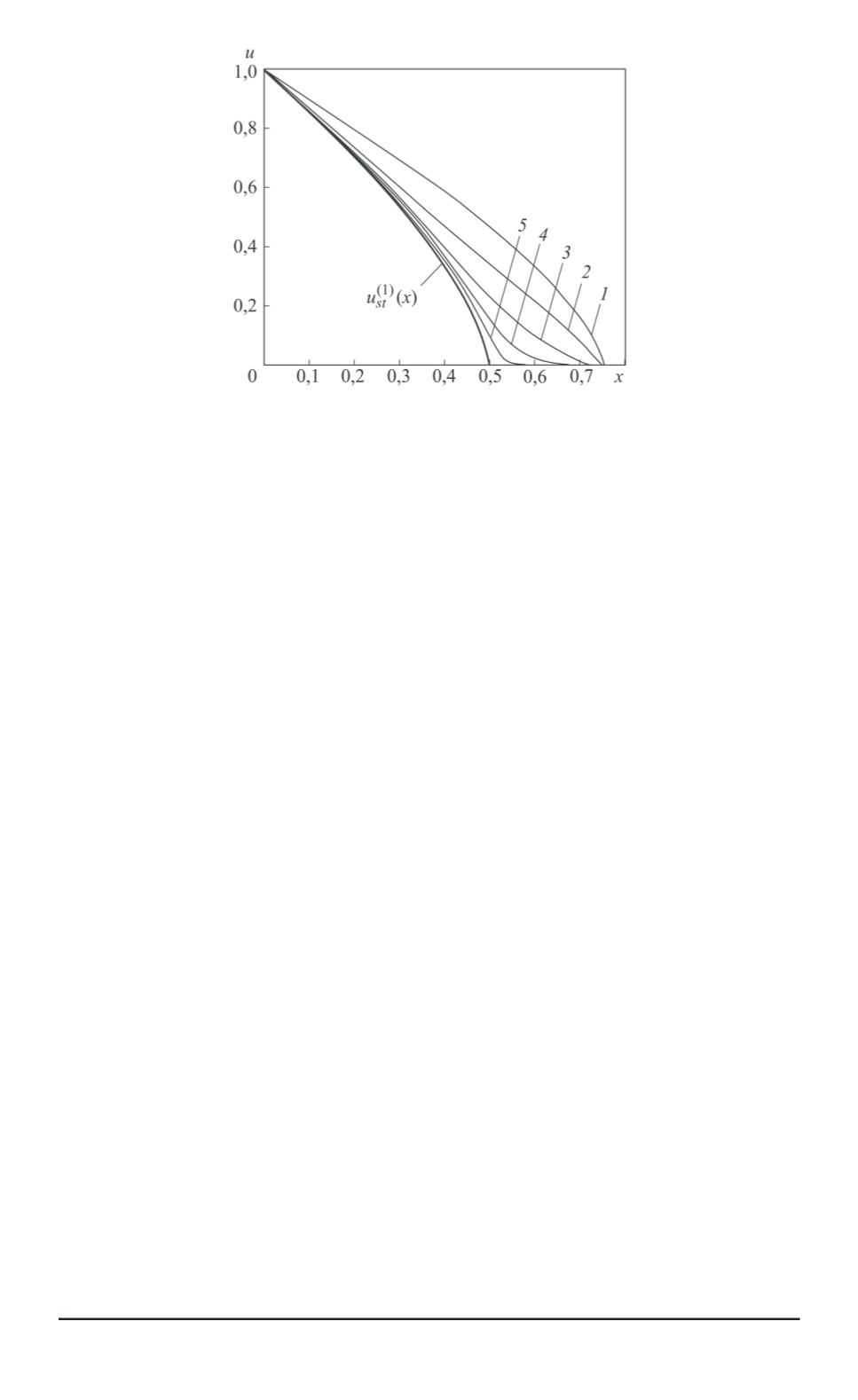
Рис. 5. Эволюция теплового возмущения в слое, когда
ϕ
(
x
)
> u
(1)
st
(
x
)
при
t
1
= 0
,
01
c (
1
),
t
2
= 0
,
1
c (
2
),
t
3
= 0
,
2
c (
3
),
t
4
= 0
,
3
c (
4
) и
t
5
= 0
,
4
c (
5
) и стацио-
нарный профиль
u
(1)
st
(
x
)
чивым предельным распределением температуры в слое при любых
начальных условиях.
Выводы.
Численное решение краевой задачи (1) подтверждает те-
оретический вывод о том, что при некоторых значениях параметров
задачи в процессе эволюции тепловых возмущений от нагретой стенки
наблюдаются нелинейные эффекты конечной скорости распростране-
ния фронта тепловой волны и пространственной локализации тепло-
вых возмущений.
ЛИТЕРАТУРА
1.
Мартинсон Л.К.
,
Малов Ю.И.
Дифференциальные уравнения математической
физики. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 368 с.
2.
Мартинсон Л.К.
Исследование математической модели процесса нелинейной
теплопроводности в средах с объемным поглощением. В кн.: Математическое
моделирование. Процессы в нелинейных средах. М.: Наука, 1986. С. 279–309.
3.
Маслов В.П.
,
Данилов В.Г.
,
Волосов К.А.
Математическое моделирование про-
цессов тепломассопереноса. М.: Наука, 1987. 362 с.
4.
Мартинсон Л.К.
,
Чигир¨eва О.Ю.
Пространственная локализация тепловых
возмущений в нелинейном процессе теплопроводности // Вестник МГТУ
им. Н.Э. Баумана. Сер. Естественные науки. 2013. № 4. С. 27–33.
5.
Мартинсон Л.К.
,
Чигир¨eва О.Ю.
Краевые задачи для квазилинейных уравнений
параболического типа // Необратимые процессы в природе и технике: Труды
Седьмой Всероссийской конференции. В 3 ч. М., 2013. Ч. II. С. 32–33.
6.
Самарский А.А.
,
Галактионов В.А.
,
Курдюмов С.П.
,
Михайлов А.П.
Режимы
с обострением в задачах для квазилинейных параболических уравнений. М.:
Наука, 1987. 480 с.
7.
Тихонов А.Н.
,
Самарский А.А.
Уравнения математической физики. М.: Изд-во
МГУ, 2004. 798 с.
8.
Самарский А.А.
Теория разностных схем. М.: Наука, 1977. 656 с.
9.
Амосов А.А.
,
Дубинский Ю.А.
,
Копченова Н.В.
Вычислительные методы для
инженеров. М.: Высш. шк., 1994. 544 с.
22
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
















