
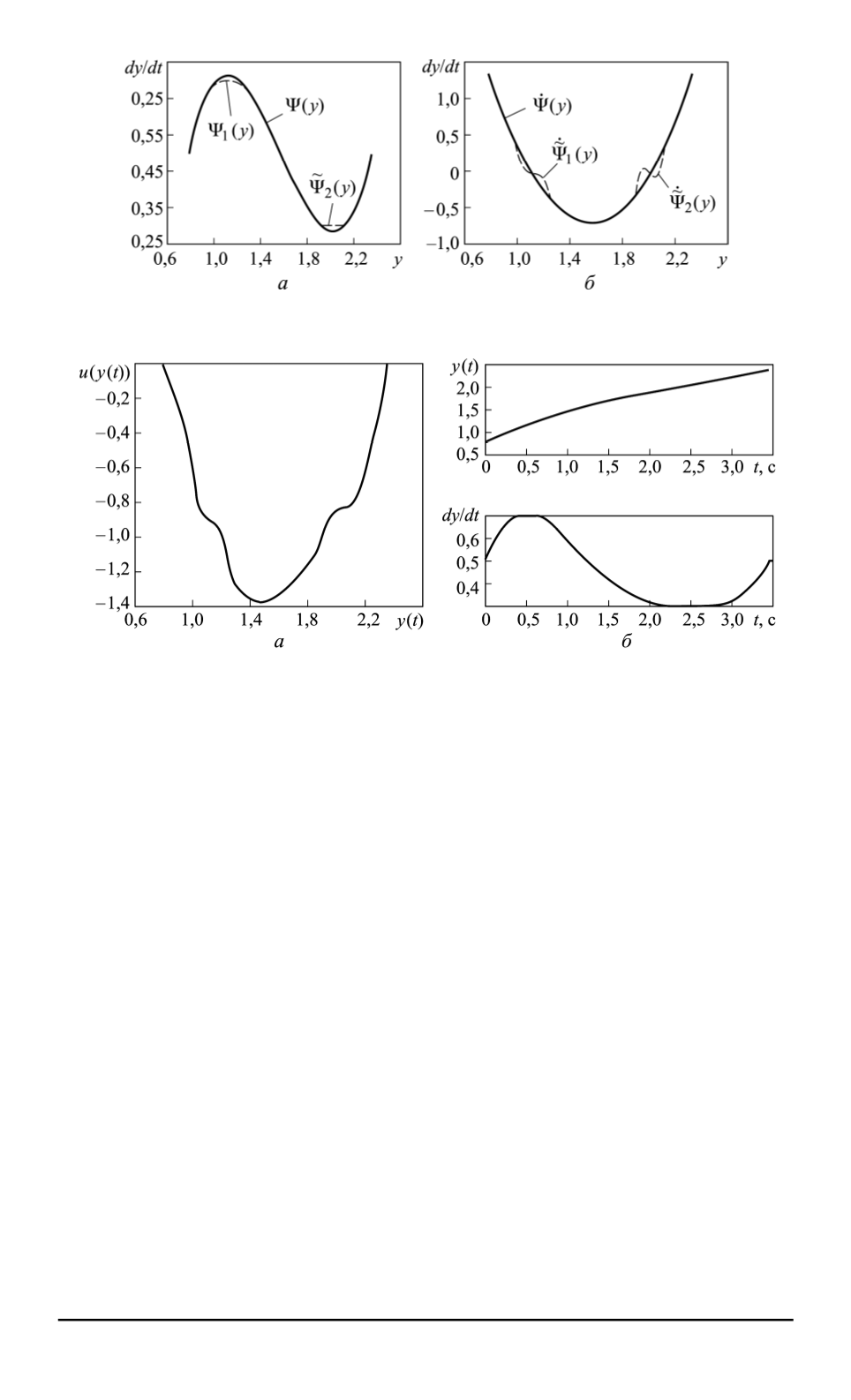
Рис. 1. Зависимости функции
Φ(
y
)
(
а
) и производной функции
Φ(
y
)
(
б
)
Рис. 2. Управление (
а
), реализующее движение по фазовой кривой, и траекто-
рия (
б
), определенная для системы (14)
на отрезке
[˜
y
l
1
; ˜
y
r
1
] = [0
,
9802; 1
,
2629]
и функцией
˜Ψ
2
(
y
) = Ψ(
y
) +
+
d
2
ψ
2
(
y
)
,
d
2
= 93
,
24
— на отрезке
[˜
y
l
2
; ˜
y
r
2
] = [1
,
9069; 2
,
1363]
(рис. 1).
Функция
Φ(
y
)
удовлетворяет условию
0
,
3
<
Φ(
y
)
<
0
,
7
,
y
∈
[
y
0
;
y
∗
]
.
Управление, реализующее движение вдоль фазовой кривой
˙
y
= Φ(
y
)
,
представлено на рис. 2,
а
. Сплошной линией построено управление,
обеспечивающее движение по фазовой траектории
˙
y
= Ψ(
y
)
, штрихо-
вой — управления, которые реализуют движения по фазовым кривым
˙
y
= ˜Ψ
1
(
y
)
и
˙
y
= ˜Ψ
2
(
y
)
.
Траектория, определенная для системы (14), которая удовлетворя-
ет условиям (15) и (16), приведена на рис. 2,
б
. Время движения из
начального состояния в конечное вдоль фазовой кривой
˙
y
= Φ(
y
)
со-
ставляет
t
∗
= 3
,
4667
c.
Заключение.
Изложено решение задач терминального управления
при наличии ограничений на состояния для систем второго поряд-
ка регулярного канонического вида. Построена функция, определяю-
щая кривую на фазовой плоскости, движение вдоль которой является
решением терминальной задачи без ограничений. Описан алгоритм
модификации построенной функции таким способом, чтобы соответ-
ствующая ей новая фазовая кривая удовлетворяла наложенным огра-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 1
23
















