
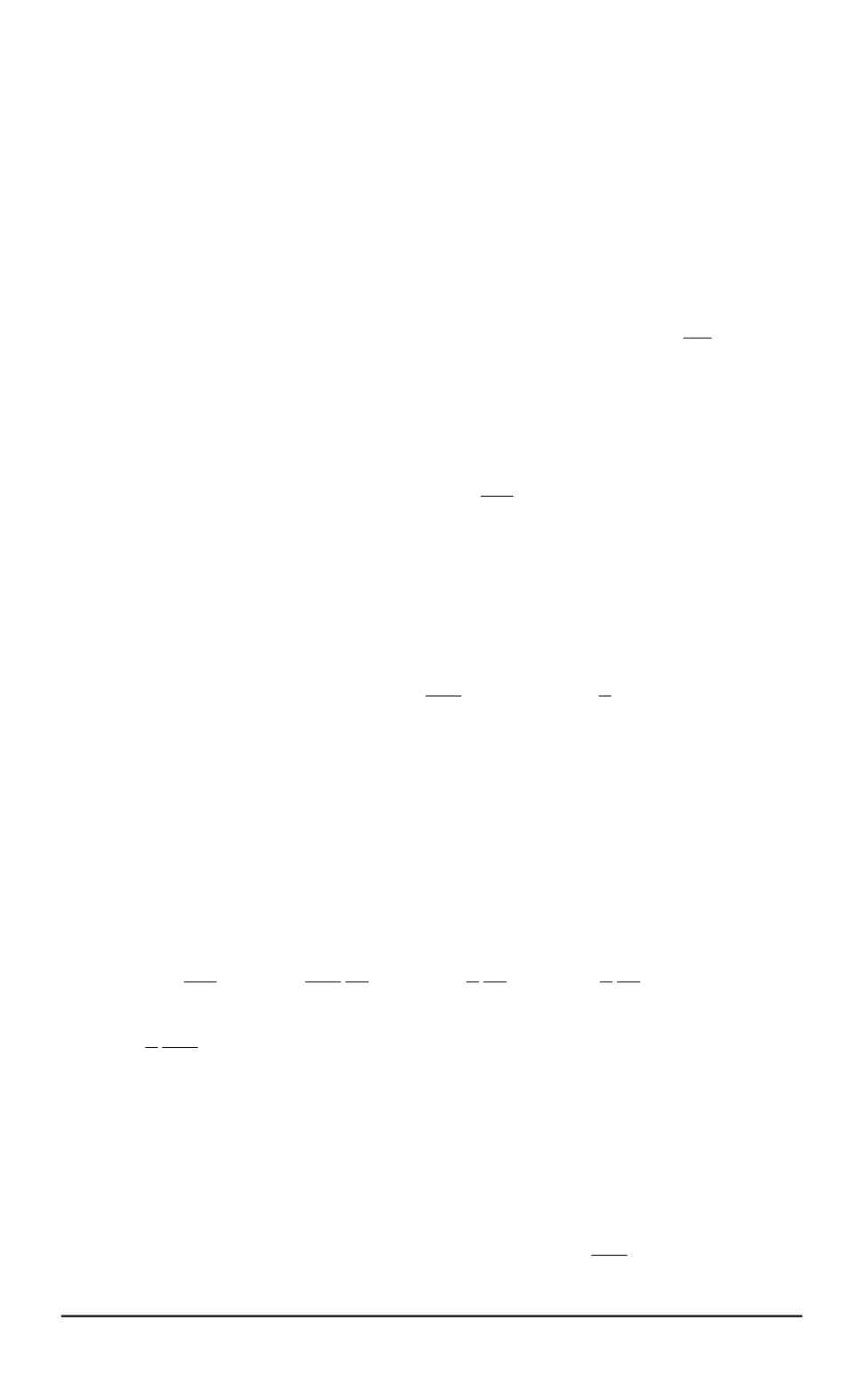
атомных электронов можно принять правило квантования Бора –
Зоммерфельда и потребовать, чтобы для каждого сверхпроводящего
электрона выполнялось условие [6]:
I
L
~p
s
d~l
=
n
~
, т.е.
I
L
e
Λ
~jd~l
+
+
I
L
e ~Ad~l
=
I
L
e
Λ
~jd~l
+
e
Ψ =
n
~
, где
Ψ
— полный магнитный поток.
На больших расстояниях от отверстия, превышающих глубину прони-
кания поля, первое слагаемое близко к нулю. Тогда получаем правило
квантования магнитного потока в сверхпроводниках:
Ψ =
n
~
e
.
Как неоднократно упоминалось [7], уравнения Максвелла являют-
ся универсальными, поэтому в случае сверхпроводников можно ввести
скалярный и векторный потенциалы по стандартным формулам
~E
=
−∇
ϕ
−
∂ ~A
∂t
;
~B
=
rot
~A.
(4)
Далее из второго уравнения Лондонов (3) с учетом (2) определяем
0 =
rot
Λ
~j
+
~B
=
rot
Λ
~j
+
rot
~A
=
=
rot
Λ
~j
+
~A
=
rot
m
e
2
n
en~v
+
~A
=
1
e
rot
m~v
+
e ~A .
Краткая запись полученного соотношения имеет вид rot
~p
s
= 0
, где
~p
s
=
e
Λ
~j
+
e ~A
=
m~v
+
e ~A
(5)
так называемый канонический импульс сверхпроводящего электрона
в электромагнитном поле.
Обратимся к первому уравнению Лондонов (1) и с помощью (2),
(4) и (5) запишем следующие соотношения:
−∇
ϕ
−
∂ ~A
∂t
=
~E
=
m
e
2
n
∂
∂t
(
en~v
) =
1
e
∂
∂t
(
m~v
) =
1
e
∂
∂t
~p
s
−
e ~A ,
отсюда
1
e
∂~p
s
∂t
=
−∇
ϕ.
С помощью последнего соотношения получается закон сохранения
флуксоида
Φ
C
=
I
C
Λ
~jd~l
+
Z
S
~Bd ~S
=
=
I
C
Λ
~jd~l
+
Z
S
rot
~Ad ~S
=
I
C
Λ
~j
+
~A d~l
=
I
C
m
e
2
n
en~v
+
~A d~l
=
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
45
















