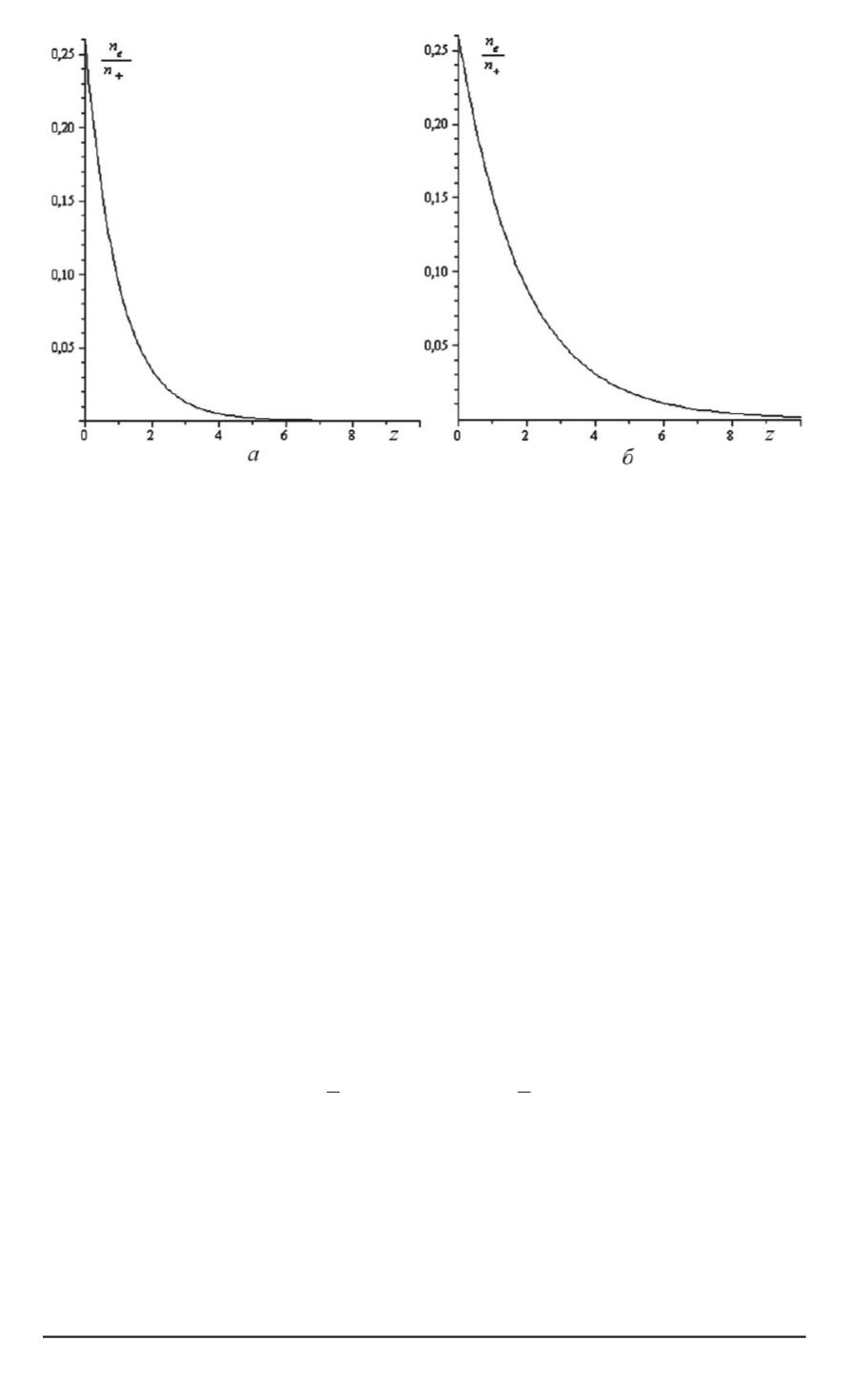
Рис. 1. Нормированное решение для плотности вырожденного электронного
газа с использованием приближения Смита в области
z
>
0
.
Расстояние
выражено в атомных единицах (для модели однородного фона):
a
—
r
s
= 4
, β
= 1
,
27
, T
= 0
K,
E
F
= 3
,
23
eV
;
б
—
r
s
= 4
, β
= 1
,
27
, T
= 3
,
5
·
10
4
K,
E
F
= 3
,
23
eV
Второе слагаемое в (5) учитывает обменные эффекты. Для их опи-
сания использовалось приближение для обменного потенциала, по-
лученное Слэтером[10]. Корреляционные эффекты не учитываются,
так как их описание носит довольно сложный характер и в большин-
стве случаев обменные эффекты вносят больший вклад в процессы,
протекающие в электронномгазе.
Результатомреализации данной схемы расчета является пошаговое
уточнение одночастичного эффективного потенциала
V
ee
[11].
Поскольку плотность электронного газа определяет одночастич-
ный эффективный потенциал, то последовательный учет вклада ка-
ждого электрона в потенциал позволяет определить
n
(
r , T
)
.
В качестве начального приближения для дальнейших расчетов бы-
ла выбрана электронная плотность, полученная Смитом [12]:
n
0
(
z
) = (1
−
1
2
e
βz
)
n
+
Θ(
−
z
) +
1
2
n
+
e
−
βz
Θ(
z
)
,
где
n
+
представляет собой среднюю плотность положительного заряда
ионной решетки.
Используемое начальное приближение позволяет при решении си-
стемы уравнений (1a), (3) применять методы решения задачи о ча-
стице, находящейся в прямоугольной потенциальной яме конечной
глубины [13].
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 1
23


