
S. Persheyev, D.A. Rogatkin
92
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
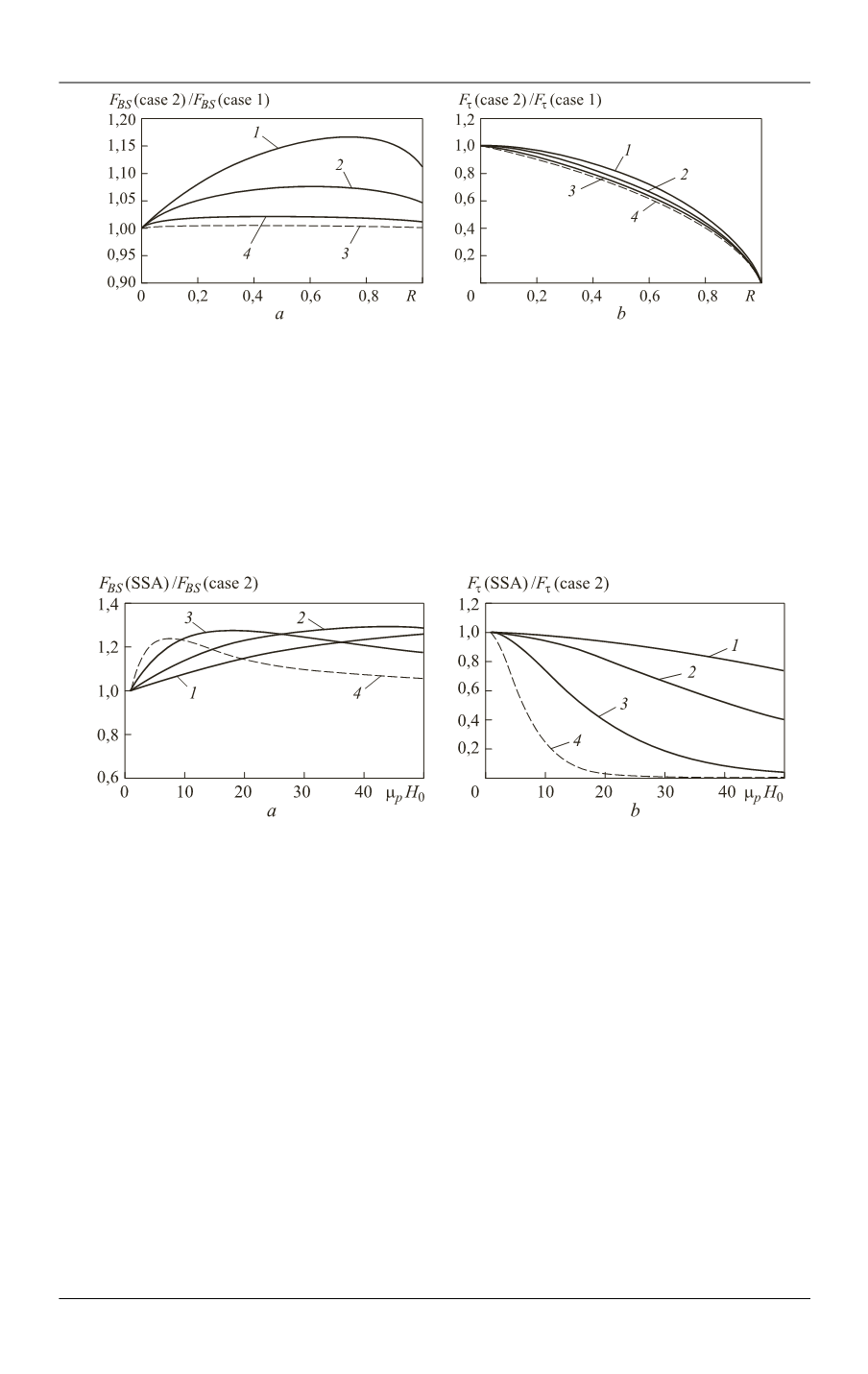
Fig. 8.
Differences in backscattered (
a
) and transmitted (
b
) fluxes for two cases of multiple
scattering model:
1
—
0
H
= 2;
2
—
0
H
= 5;
3
—
0
H
= 20;
4
—
0
H
= 100
Much stronger differences can be found if to compare solutions for MSA given
by Eqs. (26), (27), (36) (case 2) with the similar solutions for SSA given by Eqs. (21),
(22), i. e., with the use of both different scattering models and different scattering co-
efficients. These results are presented in Fig. 9.
Fig. 9.
Differences in backscattered (
a
) and transmitted (
b
) fluxes for SSA and the case 2
of MSA:
1
—
R
= 0.02;
2
—
R
= 0.04;
3
—
R
= 0.1;
4
—
R
= 0.25
As one can see, there are overestimated backscattered fluxes and, therefore,
underestimated transmitted fluxes at SSA. The multiple scattering affects like a
translucent factor at zero absorption.
Now, at the end of this section on pure scattering, as the first important
conclusion we have to put the main question. We considered the same medium Fig. 5,
the same problem of computing backscattered and transmitted fluxes, with the use of
two different approaches: SSA and MSA. However, we obtained two different
scattering coefficients Eqs. (22) and (36). Which one is correct, and which one is
wrong? The medium cannot have two scattering coefficients at the same time.
Therefore, only one answer is true: the scattering coefficient is a mathematical
parameter of the approach used, of the approximation, not of the medium. The
medium just has real physical parameters such as
R
,
H
0
and
.
Scattering coefficient
















