а
Δ
N
(
z
)
— изменение осевой силы, связаное с изменением осевой
деформации:
Δ
N
=
E
Δ
ε
z
F
(
z
);
(15)
F
(
z
) =
πδ
т
(
D
−
δ
т
)
— площадь поперечного сечения металла трубы;
осевая деформация
Δ
ε
z
связана с поперечными и продольными пере-
мещениями участка трубопровода в каждом сечении
z
.
Окончательно формулу (13) запишем в виде
N
(
z
) = (
μσ
кц
−
α
Δ
tE
+
E
Δ
ε
z
)
F
(
z
)
.
(16)
Продольная сила может изменяться под действием процессов в
грунте вокруг трубопровода и при поперечном изгибе трубопровода
как следствие некоторого удлинения.
Численное решение задачи
получено с использованием следую-
щего алгоритма.
1. В качестве исходных данных принимается прямолинейный уча-
сток трубопровода (
−
1
-я итерация метода прогонки). Фактическое
ПВП в расчетной схеме задается начальными смещениями узлов (ну-
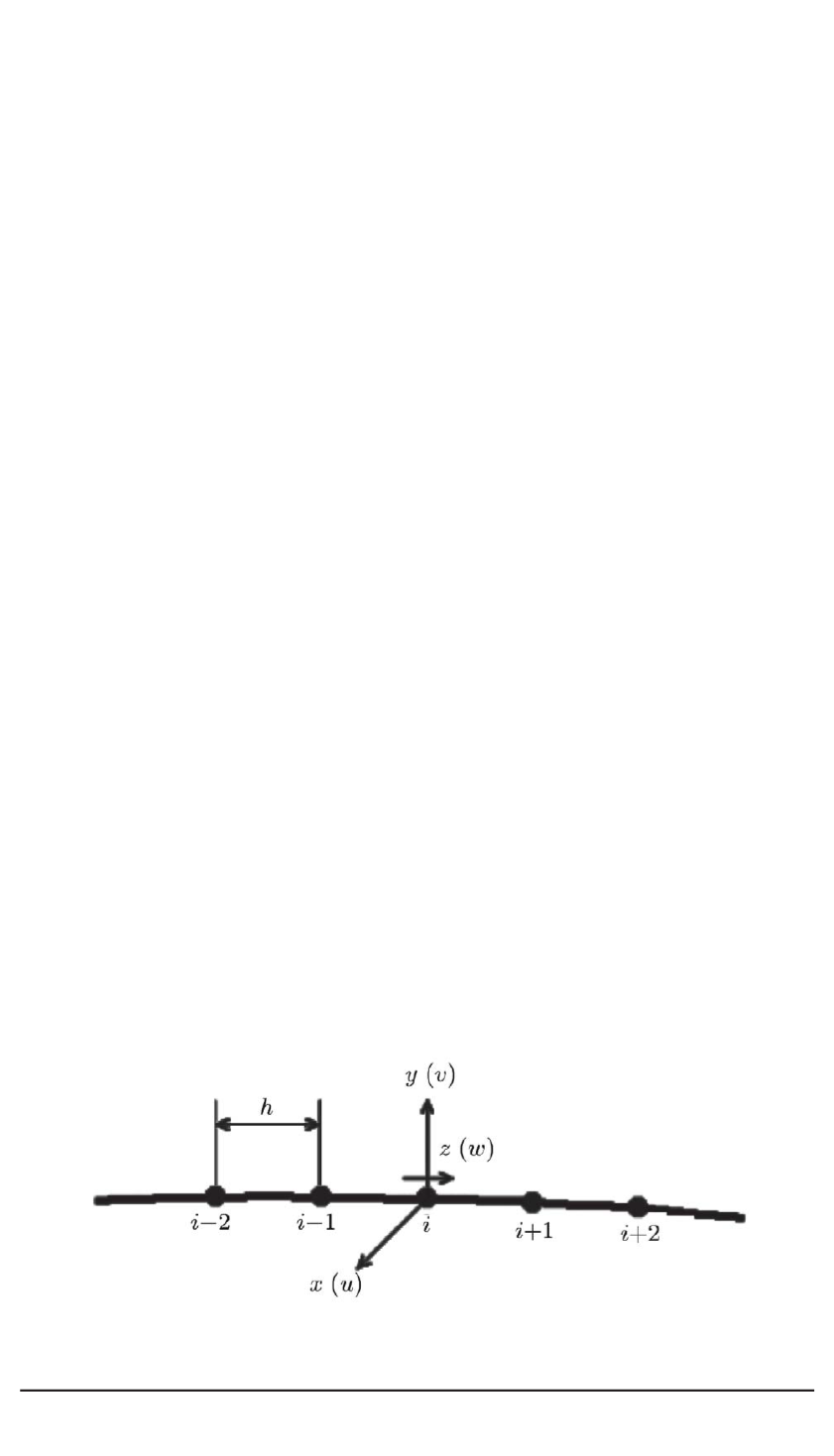
левая итерация метода прогонки). Внутри участка строится конечно-
элементная сетка с размером элементов
h
(рис. 3).
2. Реализуется итерационный процесс (прогонка) (
j
=
−
1
,
0
,
2
,
3
, . . .
. . . , p
) в пределах всех узлов конечно-элементной модели (
i
= 1
,
2
,
3
, . . . , n
) и определяется результирующее смещение каждого узла
(
i
) посредством формул, полученных при решении системы уравне-
ний (1),
u
j
+1
i
=
A
j
ui
u
j
i
−
1
+
u
j
i
+1
+
B
j
ui
u
j
i
−
2
+
u
j
i
+2
+
C
j
ui
;
v
j
+1
i
=
A
j
vi
v
j
i
−
1
+
v
j
i
+1
+
B
j
vi
v
j
i
−
2
+
v
j
i
+2
+
C
j
vi
;
w
j
+1
i
= 0
,
5
w
j
i
−
1
+
w
j
i
+1
+
C
j
wi
,
(17)
Рис. 3. Расчетная схема участка трубопровода
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 3
105


