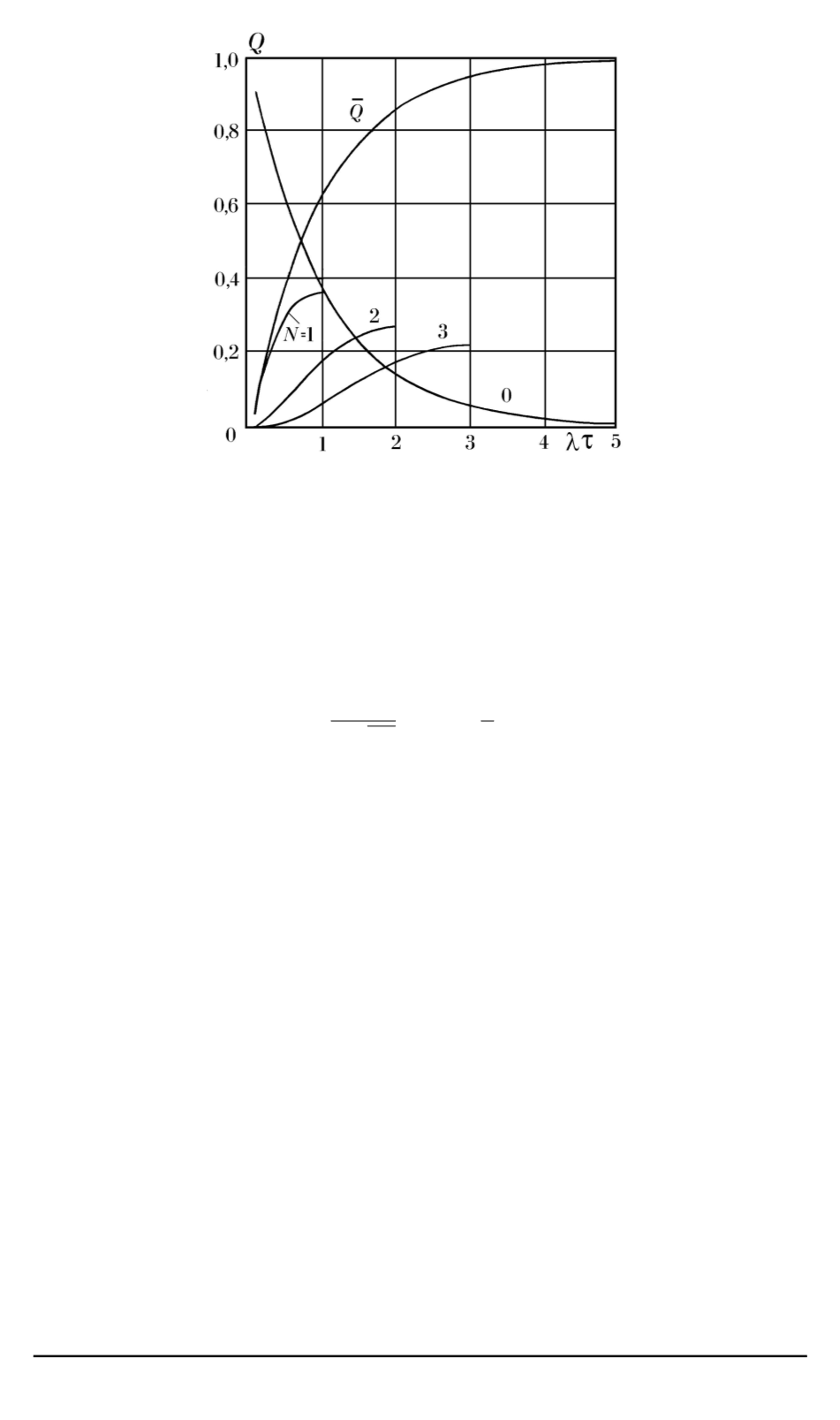
Рис. 1. Вероятность аварий и оценка риска
ˉ
Q
аварийности в зависимости от
параметра
λτ
На рис. 2 показано распределение Пуассона для нескольких значе-
ний параметра
λτ
, из которого следует, что при больших значениях
λτ
(
λτ
>
10
) распределение приближается к нормальному распреде-
лению при
μ
=
σ
2
=
λτ
f
(
x, μ, σ
) =
1
σ
√
2
π
exp
−
1
2
(
x
−
μ
)
2
σ
2
.
Для ведения оценки надежности сейсмостойкости МТ необходи-
мо статистическое описание сейсмических свойств (модели) грунта.
Предлагались различные модели математического описания колеба-
ний грунта при землетрясениях. Широкое распространение получила
модель В. Болотина [1, 2], основанная на представлении ускорений
¨
Z
в форме, позволяющей учесть изменение во времени спектрального
состава колебаний:
¨
Z
(
t
|
s
) =
X
k
L
k
(
t
|
s
)
ϕ
k
(
t
|
s
)
.
(3)
Здесь
s
— вектор, характеризующий интенсивность сотрясения, спек-
тральный состав, продолжительность интенсивной фазы (зависит от
макросейсмических параметров, местных геологических и грунтовых
условий);
L
k
— квазиогибающие, характеризующие медленное изме-
нение амплитуд во времени на отрезке
θ
преобладающих периодов
сотрясения и нулевые вне отрезка длительности сотрясения
θ
;
ϕ
k
—
стационарные случайные функции времени, характеризующие спек-
тральный состав сотрясения, с нулевым математическим ожиданием
и единичной дисперсией.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4
57


