H
∗
α
(0)
i
= ¯
H
∗
i
+
v
∗
α
(1)
|
i
= ¯
H
∗
i
−
¯
H
∗
i
+
3
p
=1
ϑ
∗
α
(
p
)
|
i
=
3
p
=1
ϑ
∗
α
(
p
)
|
i
.
(7)
Подставляя (6) и (7) в (3), находим, что функции
ϑ
∗
α
(
p
)
являются
решением следующей задачи:
⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
b
∗
α
i
(
p
)
/i
= 0
,
˜
V
αξ
, α
= 1
, . . . , N
;
b
α
i
(
p
)
=
μ
∗
α
H
∗
α
i
(
p
)
;
H
∗
α
i
(
p
)
=
ϑ
∗
α
(
p
)
|
i
;
ϑ
∗
α
(
p
)
=
ϑ
∗
N
(
p
)
,
b
∗
α
i
(
p
)
−
b
∗
N
i
(
p
)
n
i
= 0
на
˜Σ
ξ
αN
;
ϑ
∗
α
(
p
)
Σ
p
= 0
,
ϑ
∗
α
(
p
)
|
Σ
p
= 0
,
5 ¯
H
∗
p
;
ϑ
∗
α
(
p
)
|
q
Σ
q
= 0
,
ϑ
∗
α
(
p
)
|
q
Σ
q
= 0
,
q
=
p.
(8)
Эта задача имеет “классический” тип, поскольку при фиксирован-
ном значении
p
она состоит из уравнений Лапласа (с комплексными
неизвестными), записанных для областей
˜
V
αξ
(это пересечения обла-
стей
V
αξ
с 1/8 ЯП), с условиями идеального контакта на поверхностях
контакта
˜Σ
ξ
αN
и условиями первого или второго рода на координатных
плоскостях
Σ
p
и торцевых плоскостях
Σ
p
=
{
ξ
p
= 0
,
5
}
. Задачи (8) для
1/8 ЯП
˜
V
ξ
=
α
=1
˜
V
αξ
будем далее обозначать как задачи
L
p
.
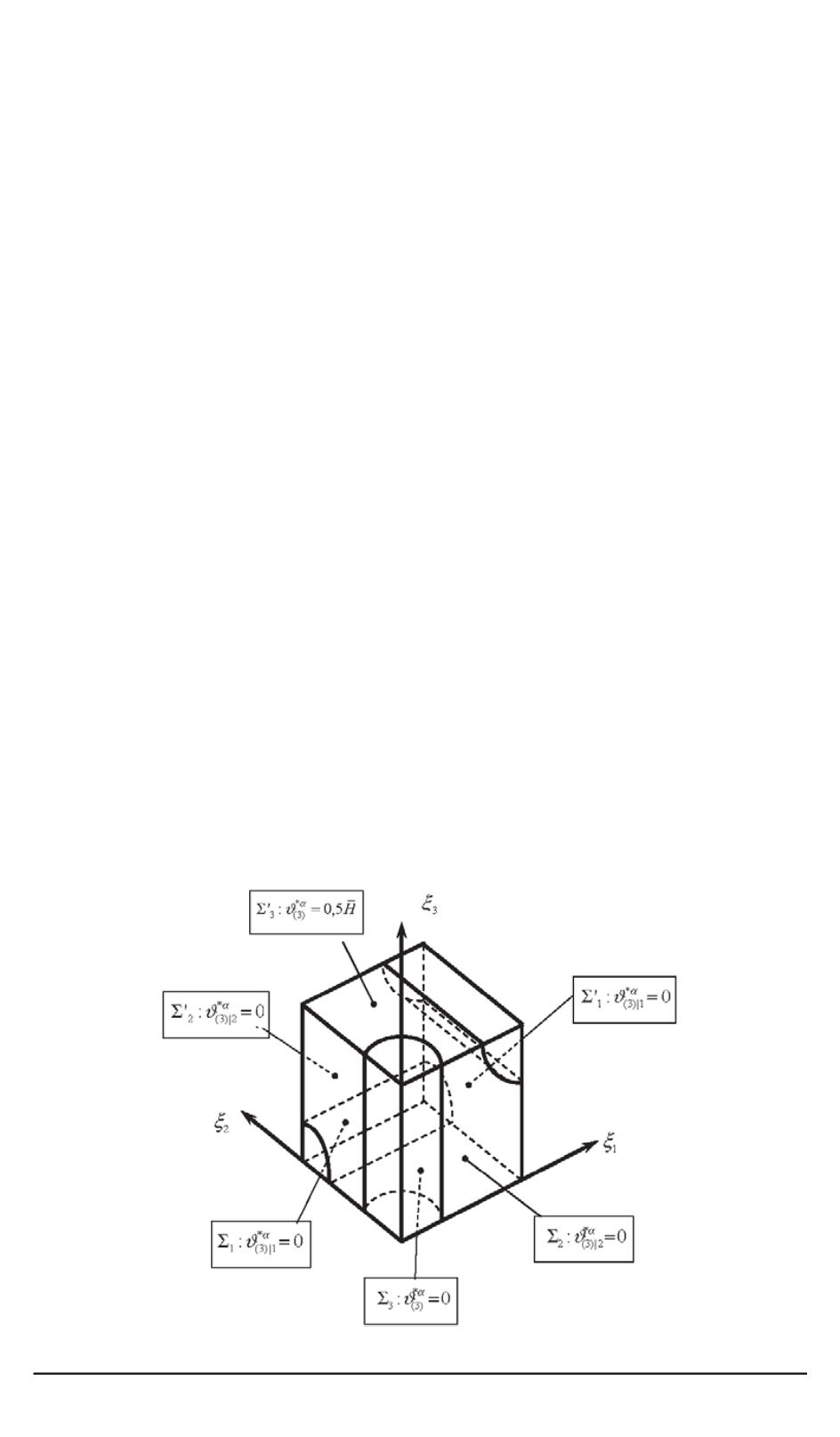
Граничные условия для задачи
L
3
показаны на рис. 2.
Расчет тензора магнитной проницаемости композиционного
материала.
Для вычисления магнитного потенциала в нулевом при-
ближении
v
∗
(0)
из (1) и (2) получаем осредненную задачу теории
Рис. 2. Граничныеусловия для задачи
L
3
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 1


