и мнимую части с привлечением QMR-методов решения СЛАУ для
возникающих в таком подходе несимметричных матриц.
Расчет для 3D ортогонально-армированного композиционного
материала.
С помощью разработанного метода решены задачи
L
p
для
3D ортогонально-армированного композита (число
N
= 4
,
α
= 1
,
2
,
3
— волокна,
α
= 4
— матрица). Число КЭ при решении задач
L
p
со-
ставляло 6343, число степеней свободы — 1502. При численной реа-
лизации учитывалось, что армирующие в трех направлениях волокна
могут состоять из различных материалов.
Проведено 10 тестовых расчетов для 3D ортогонально-армирован-
ного композиционного материала с одинаковыми волокнами (см. рис. 1
и 2) с модельными значениями коэффициентовмагнитной проница-
емости волокон и матрицы
μ
∗
f
, μ
∗
m
. Были выбраны следующие со-
отношения между
μ
∗
f
, μ
∗
m
: Re
μ
∗
m
/
Re
μ
∗
f
= 0
,
1
, Im
μ
∗
m
/
Re
μ
∗
m
= 0
,
1
,
Im
μ
∗
f
/
Re
μ
∗
f
= 0
,
1
. По формулам (10), (11) были вычислены эффек-
тивные значения коэффициента магнитной проницаемости композита.
Для сравнения проводились также вычисления вилки Фойгта–Рейсса
(линейная и обратно-линейная зависимости)
μ
∗
=
μ
∗
f
ϕ
f
+
μ
∗
m
(1
−
ϕ
f
);
1
μ
∗
=
ϕ
f
μ
∗
f
+
(1
−
ϕ
f
)
μ
∗
m
,
(18)
где
ϕ
f
— коэффициент армирования.
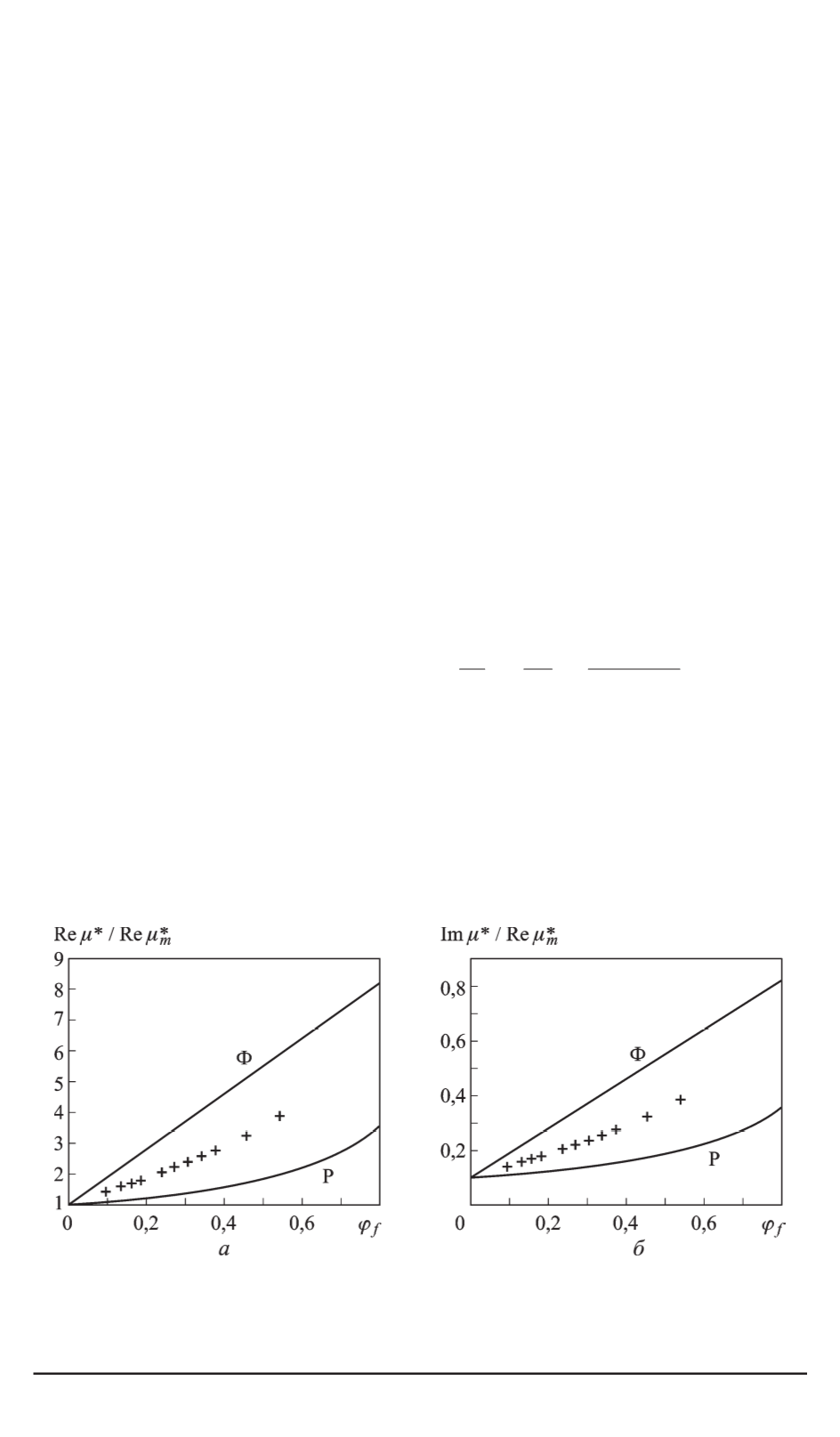
На рис. 3,
а
изображена действительная часть коэффициента маг-
нитной проницаемости композита Re
μ
∗
взависимости от
ϕ
f
, на
рис. 3,
б
— мнимая часть Im
μ
∗
, а на рис. 4 — абсолютная величина
|
μ
∗
|
.
Результаты расчетовпоказывают, что значения Re
μ
∗
, Im
μ
∗
и
|
μ
∗
|
для
3D ортогонального композита укладываются в вилку Фойгта–Рейсса,
Рис. 3. Зависимости действительной (
а
) и мнимой (
б
) частей магнитной про-
ницаемости 3D композита от коэффициента армирования, рассчитанные по
методу Фойгта–Рейсса (Ф, Р) и методом асимптотического осреднения (звездоч-
ки)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 1
9


