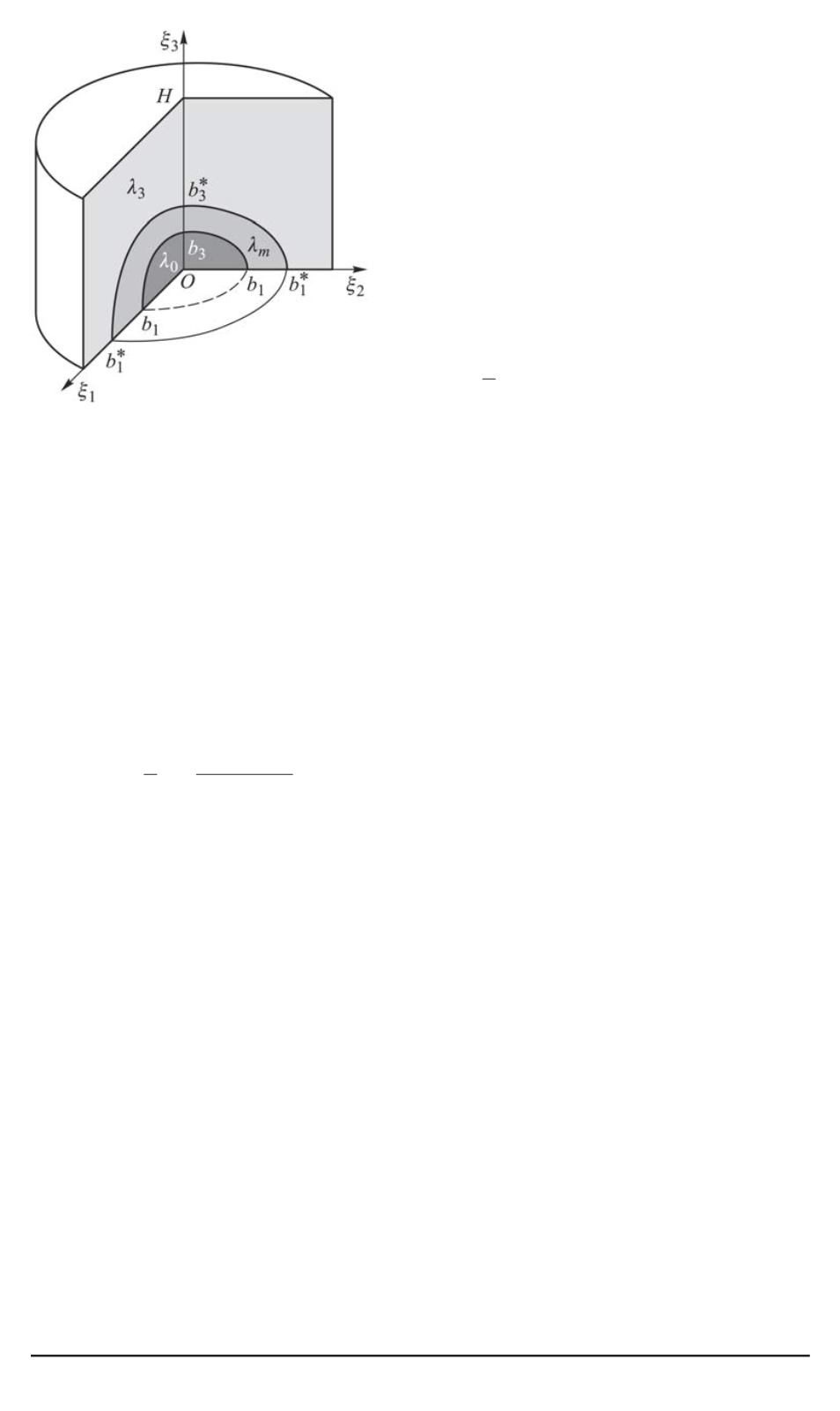
Рис. 1. Модель композита со сфе-
роидальными включениями
цилиндрической области объемом
V
0
=
HS
0
, ограниченной поверхно-
стью
S
, распределение температуры
T
(
M
)
и коэффициент теплопроводно-
сти
λ
(
M
)
являются функциями коор-
динат точки
M
∈
V
, причем функция
λ
(
M
)
кусочно постоянна в каждой из
подобластей области
V
(см. рис. 1).
В качестве допустимого длямини-
мизируемого функционала [8]
J
[
T
] =
1
2
V
λ
(
M
)
∇
T
(
M
)
2
dV
(
M
)
,
M
∈
V,
(13)
примем линейное по высоте цилинд-
ра распределение температуры с постоянной составляющей градиента
T,
◦
3
(
∇
— дифференциальный оператор Гамильтона). Тогда из (13) по-
лучим
2
J
1
[
T
]
/
(
T,
◦
3
)
2
=
λ
3
(
HS
0
−
2
π
ˆ
b
2
1
ˆ
b
3
/
3)+
+2
πλ
m
( ˆ
b
2
1
ˆ
b
3
−
b
2
1
b
3
)
/
3 + 2
πλ
0
b
2
1
b
3
/
3
.
(14)
Длямаксимизируемого функционала [8]
I
[q] =
−
1
2
V
q(
M
)
2
λ
(
M
)
dV
(
M
)
−
S
T
(
P
)q(
P
)n(
P
)
dS
(
P
)
, P
∈
S,
(15)
в качестве допустимого распределениявектора плотности теплового
потока
q
примем постоянное значение единственной составляющей
этого вектора
q
=
−
λ
3
T,
◦
3
, перпендикулярной основаниям цилиндра
(
n
— единичный вектор внешней нормали к поверхности
S
). В этом
случае из (15) следует, что
2
I
1
[
q
]
/
(
λ
3
T,
◦
3
)
2
=
−
(
HS
0
−
2
π
ˆ
b
2
1
ˆ
b
3
/
3)
/λ
3
−
2
π
( ˆ
b
2
1
ˆ
b
3
−
b
2
1
b
3
)
/
(3
λ
m
)
−
−
2
πb
2
1
b
3
/
(3
λ
0
) + 2
HS
0
/λ
3
.
(16)
Использованные допустимые распределениятемпературного поля
и плотности теплового потока длянеоднородной области отличаются
от действительных распределений, поэтому значения
J
1
[
T
]
и
I
1
[
q
]
не
будут совпадать, причем
J
1
[
T
]
> I
1
[
q
]
. В промежутке между этими
значениями должно быть расположено значение
J
0
=
λ
3
(
T,
◦
3
)
2
HS
0
/
2
минимизируемого функционала (13) дляоднородной области с коэф-
фициентом теплопроводности
λ
3
. Тогда при
b
2
1
b
3
/
( ˆ
b
2
1
ˆ
b
3
) = 1
/C
3
∗
=
C
V
122
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4


