Модификации алгоритмов статистического моделирования пе-
реноса электронов.
Естественным обобщением методов статистиче-
ского моделирования, в основе которых лежит предварительный рас-
чет плотности распределений характеристик электронных потоков,
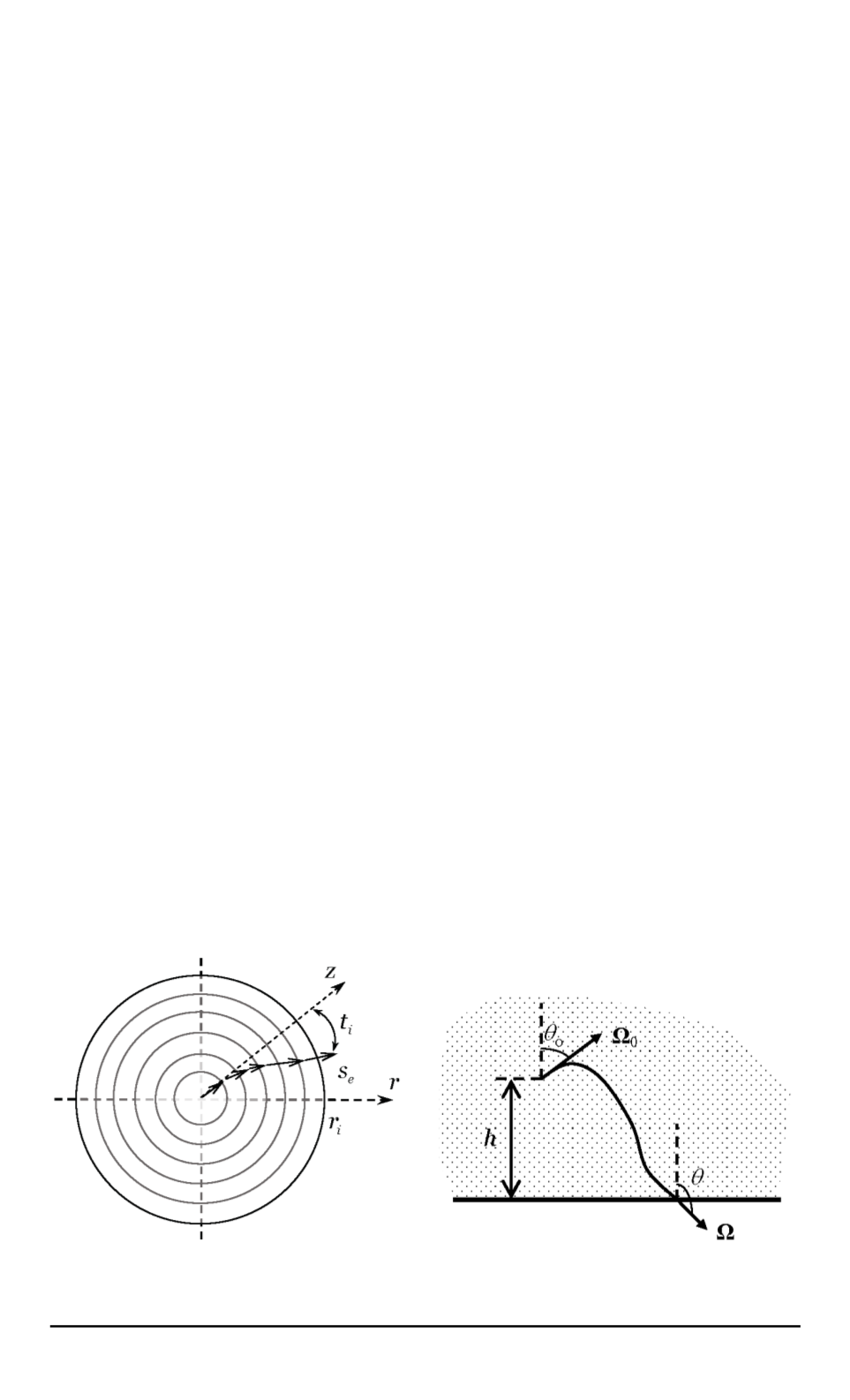
может служить следующий подход (рис. 7).
Вводится дискретная сетка по
r
(
{
r
i
}
I
i
=0
=
{
r
0
, . . . , r
I
=
λ
(
ε
0
)
}
;
λ
(
ε
0
)
— тормозная способность электрона с энергией
ε
,
r
0
= 0
—
начало траектории). На этой сетке путем моделирования траектории
движения электрона
s
e
(начальное направление движения электрона
совпадает с направлением оси
z
) рассчитывается (например, с исполь-
зованием модели “утолщенных” траекторий) многомерная плотность
распределения
f
(
r,
Ω
, ε, t
|
ε
0
)
, где
ε
0
, ε
— начальная и текущая энергии
электрона;
Ω
— текущее направление движения электрона;
t
— попе-
речное смещение. Эта функция может многократно использоваться
для решения задач о переносе электронов в различных постановках.
В качестве другой модификации обсуждаемых алгоритмов рассмо-
трим следующий подход для решения задачи об электронной эмиссии
из плоского приграничного слоя объекта под действием ионизирую-
щего излучения. Такие задачи актуальны во многих практических при-
ложениях [18]. Статистическую модель переноса электронов в пригра-
ничном материале объекта можно построить, если заранее получить
плотность распределения
f
(
E,
Ω
|
E
0
,
Ω
0
, h
)
вылетающих электронов
по глубине рождения
h
, начальной энергии
E
0
, начальному напра-
влению движения
Ω
0
, конечной энергии
E
и конечному направлению
движения
Ω
(рис. 8). Такую модель будем называть в дальнейшем ин-
женерной.
Рассмотренные многомерные функции требуют очень большого
объема памяти для хранения таблиц их значений и поэтому являются
неудобными для использования в практических задачах.
Рис. 7. Схема расчета распределения
характеристик электронных потоков
Рис. 8. Траектория электрона в при-
граничном слое объекта
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1


