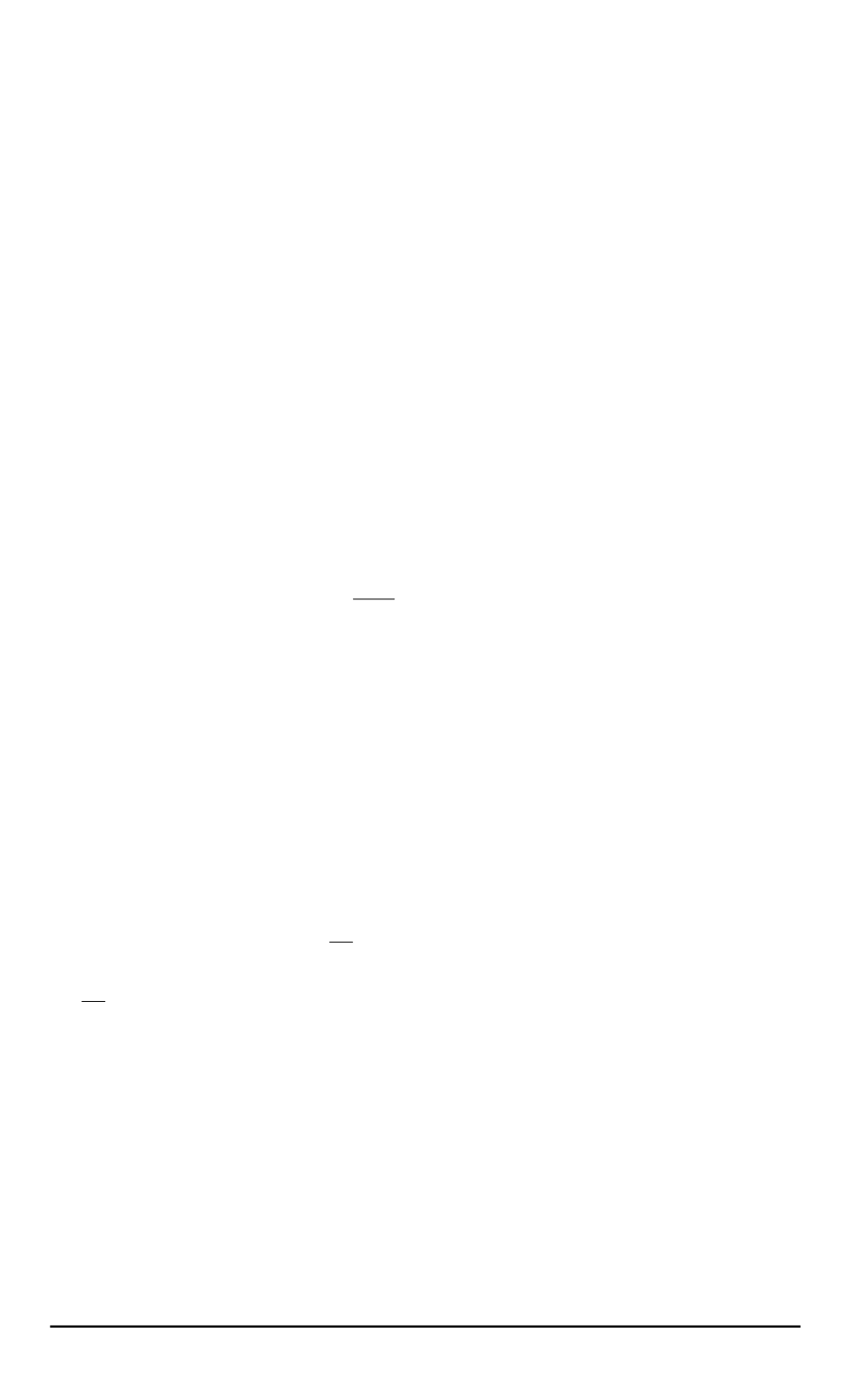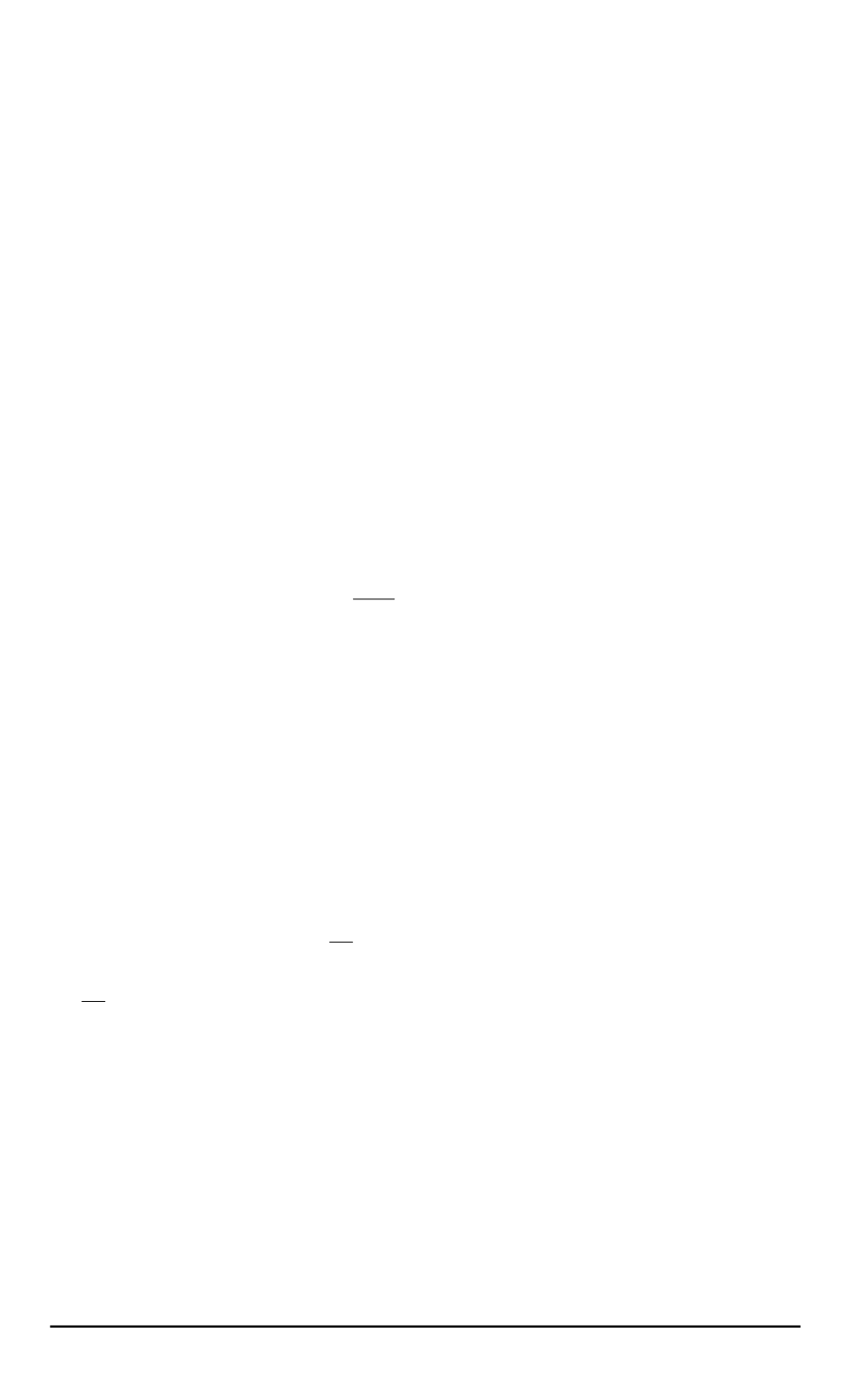
Гамильтониан модели цепочки спинов
H
=
∞
X
n
=
[
−
J
(
S
n
S
n
+1
) +
A
(
S
z
n
)
2
−
gm
B
B
x
S
x
n
]
(1)
описывает энергию ферромагнетика Гейзенберга — кристалла CsNiF
3
[3]. Здесь
m
B
— магнетон Бора;
g
— гиромагнитное отношение;
J
—
энергия обменного взаимодействия между соседними спинами
S
n
;
А
— энергия анизотропии. Внешнее магнитное поле
B
x
, направленное
вдоль оси
x
, разрушает симметрию в плоскости
xy
. Суммирование ве-
дется по бесконечной цепочке, и предполагается, что плоскость “лег-
кого намагничивания” — плоскость
xy
перпендикулярна оси цепочки
z
, вдоль которой пронумерованы атомы со спином
S
n
. Энергия анизо-
тропии
A >
0
достаточно велика, чтобы вектор спина
S
n
был заключен
преимущественно в плоскости
xy
.
Уравнение движения для проекций спинов на оси координат выра-
жается через квантовые скобки Пуассона операторов проекций спинов
и гамильтониана (1) в виде
i
~
∂S
θ
n
∂t
=
S
θ
n
, H ,
(2)
где
~
— постоянная Планка;
θ
принимает значения
x, y, z
;
S
θ
n
— проек-
ция спина на ось
θ
. Считаем спин
S
n
классическим вектором длиной
S
, направление которого определяется двумя углами —
Φ
и
α
:
S
n
=
S
(cos
α
n
cos Φ
n
,
cos
α
n
sin Φ
n
,
sin
α
n
)
.
(3)
Учтем наличие плоскости легкого намагничивания при условии,
что энергия анизотропии достаточно велика (
A gm
B
B
x
/S
) и
α
→
0
.
Используя коммутационные соотношения для проекций моментов ко-
личества движения, получим из соотношения (2) уравнения вида
~
∂
∂t
Φ
n
= 2
AS
sin
α
n
;
(4)
~
∂
∂t
α
n
=
JS
(sin(Φ
n
+1
−
Φ
n
)
−
sin(Φ
n
−
Φ
n
−
1
))
−
gm
B
B
x
sin Φ
n
.
(5)
Введем величину
а
1
=
m
B
g
В
x
/JS
нормированного внешнего маг-
нитного поля. Подставляя производную угла
α
n
, найденную из урав-
нения (4), в (5), получаем, что конфигурация бегущей волны в модели
Гейзенберга с плоскостью легкого намагничивания с гамильтонианом
(1) описывается уравнением
sin(ΔΦ
n
+1
)
−
sin(ΔΦ
n
) =
a
1
sin Φ
n
+ (
v
2
/c
2
)Φ
(2)
n
,
(6)
где
c
2
= 2
AJS
2
h
2
/
~
2
;
v
— фазовая скорость;
h
— межатомное рас-
стояние в цепочке;
ΔΦ
n
= Φ
n
−
Φ
n
−
1
и
ΔΦ
n
+1
= Φ
n
+1
−
Φ
n
;
Φ
(2)
n
—
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1
57