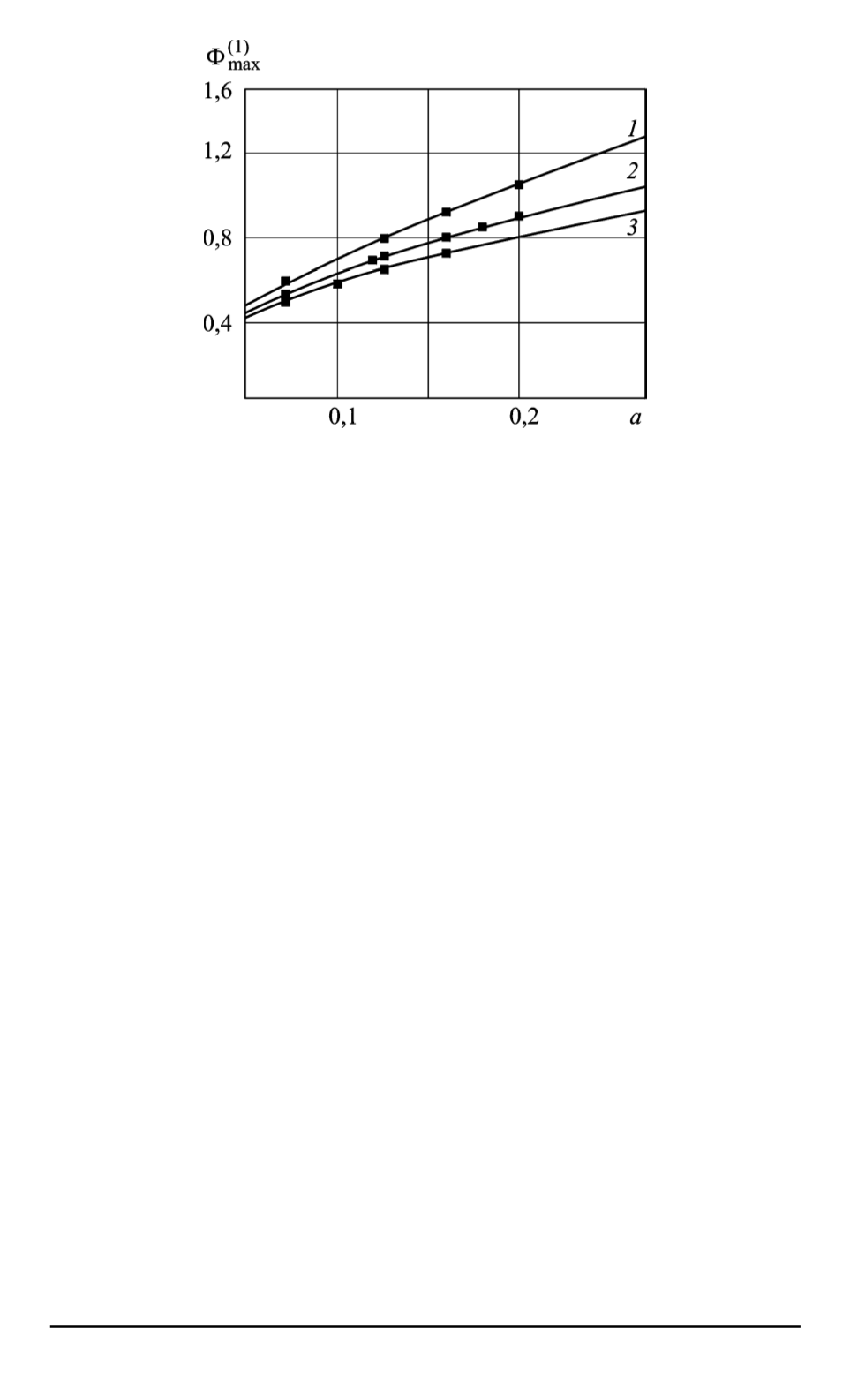
Рис. 2. Зависимости от величины поля амплитуд солитонов, найденных по урав-
нению (15) (точки — значения амплитуд, полученные по уравнению (9)):
1, 3
— солитоны растяжения и сжатия ангармонической цепи ФК (
Γ = 1
/
5
) соответ-
ственно;
2
— кинки модели ФК (
Γ = 0
)
модели ФК:
(4Γ
/B
)Φ
(1)
= 1
−
3
1
/
2
sin
s
−
cos
s,
(4Γ
/B
)Φ
(1)
<
0;
(17)
(4Γ
/B
)Φ
(1)
= 1 + 3
1
/
2
sin
s
−
cos
s,
(4Γ
/B
)Φ
(1)
>
0;
(18)
(4Γ
/B
)Φ
(1)
= 1 + 2 cos
s,
(4Γ
/B
)Φ
(1)
>
0
,
(19)
где
s
= arccos((1+
C
−
(48
a
Γ
2
/B
3
(1
−
cos Φ))
/
3)
. Первая ветвь решений
(17) должна быть отброшена при анализе цепочки спинов. Ее нет в
исходном уравнении (6), так как мы ограничились областью
Φ
(1)
>
0
.
Но остальные решения уравнения (11) связывают ферромагнетик и
ангармонизм в модели ФК [7, 8]. Для величин
(4Γ
/B
) Φ
(1)
1
урав-
нения (17) и (18) дают решения модели ФК. Третья ветвь решений (19)
может быть решением и для ферромагнетика, где ранее ее не исследо-
вали. Фазовые траектории (15) разделены сепаратрисами, отвечающи-
ми значениям констант
C
= 0
,
C
= 96
a
Γ
2
/
В
3
−
2
. При
а
=
B
3
/
48Γ
2
сепаратрисы отвечают одному значению константы интегрирования
C
= 0
, сливаются и дают профиль (16). Кинк в цепи спинов — это
солитон растяжения модели ФК с постоянной ангармонизма в цепи
Γ = 1
/π
.
Нормированная на величину
JS
2
энергия системы (1) равна
Е
=
∞
X
n
=1
(
−
(cos
α
n
cos
α
n
+1
cos(Φ
n
+1
−
Φ
n
) + sin
α
n
sin
α
n
+1
)+
+ (
A/J
) sin
2
α
n
−
(
m
B
gB
x
/JS
) cos
α
n
cos Φ
n
)
.
(20)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1
61


