Скорость солитона ограничена предельной величиной, меньшей, чем
скорость
с
длинноволновых магнонов или скорость звука в цепочке
ФК. Решения уравнения (11) могут быть получены из выражения
(4Γ
/B
)Φ
(1)
= 1+2 cos((2
πj
+arccos(1+
C
−
48
a
Γ
2
/B
3
(1
−
cos Φ)))
/
3)
,
(15)
где
j
= 0
,
1
,
2
;
С
— константа интегрирования. Для кинков
С
= 0
. Най-
денные решения позволяют вычислить амплитуды деформаций связей
Φ
(1)
max
(при
Φ =
π
)
(рис. 1, 2):
4ΓΦ
(1)
max
=1 + 2 cos((2
πj
+ arccos(1
−
96
a
Γ
2
))
/
3)
.
Из сравнения с точным численным решением дискретной задачи
(6) (см. рис. 1, 2) по этой зависимости и аналогичной для уравнения
(12) следует, что континуальное уравнение (12), с точностью до 5%
справедливо при
a <
0
,
18
, а для уравнения (11) имеем согласие с
результатами численного расчета по уравнению (6) при меньших ве-
личинах ангармонизма.
При критическом значении поля
а
= 1
/
48Γ
2
= 0
,
2056
из уравне-
ния (15) следует точно найденный профиль кинка с топологическим
зарядом 2
Φ(
z
) = 6 arctg
√
3 th
√
3
z
24Γ
.
(16)
На отрезке
0
<
Φ
<
2
π
уравнение (15) дает три ветви решений
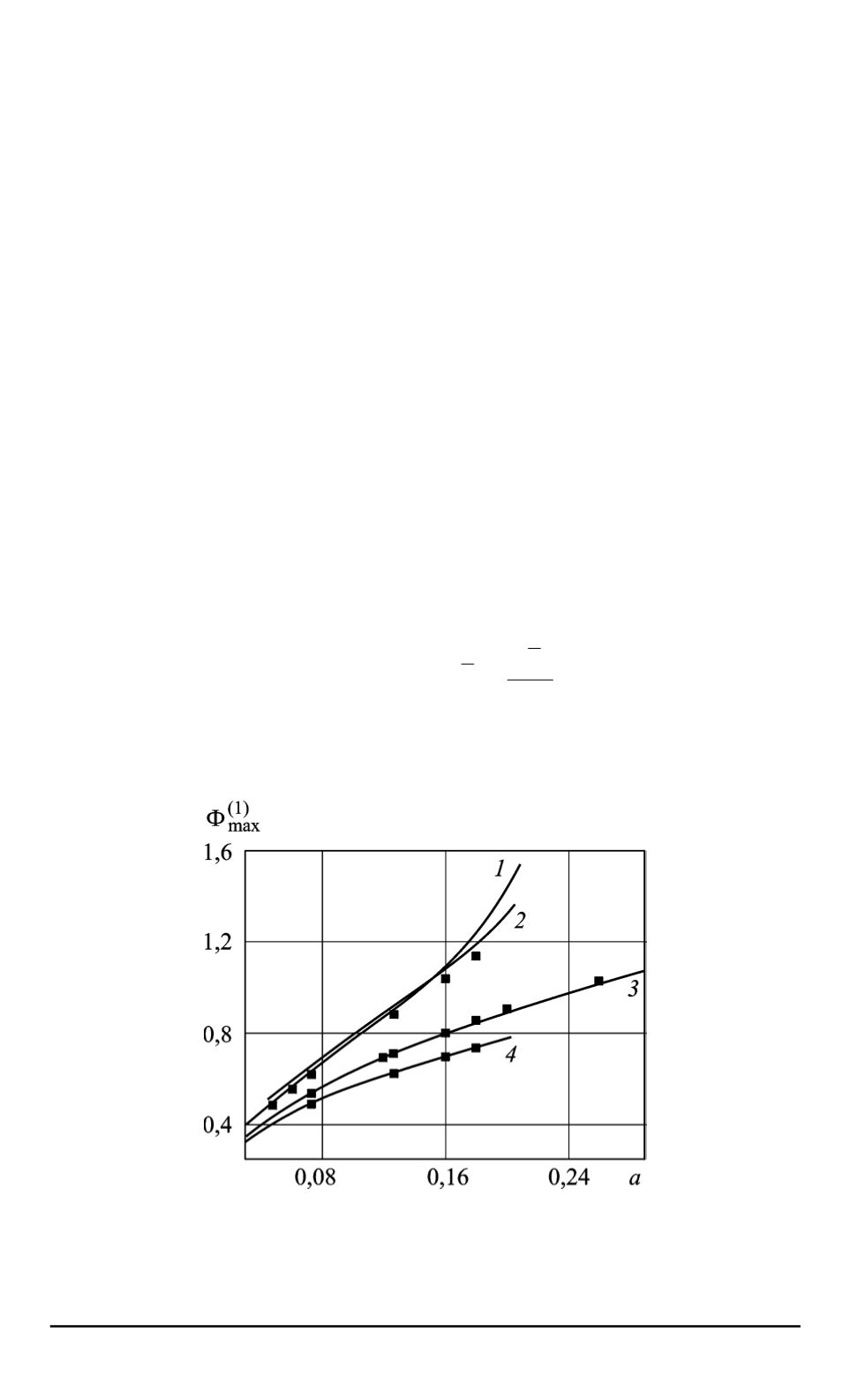
Рис. 1. Зависимости амплитуд солитонов от величины поля:
1, 4
— амплитуды, найденные по уравнению (15) для солитона растяжения и сжатия
ангармонической цепочки ФК (
Γ = 1
/π
) соответственно (точки — значения ампли-
туд, полученные по уравнению (9));
2
— амплитуды, найденные по уравнению (12)
для кинка в магнетике;
3
— кинки модели ФК (
Γ = 0
)
60
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1


