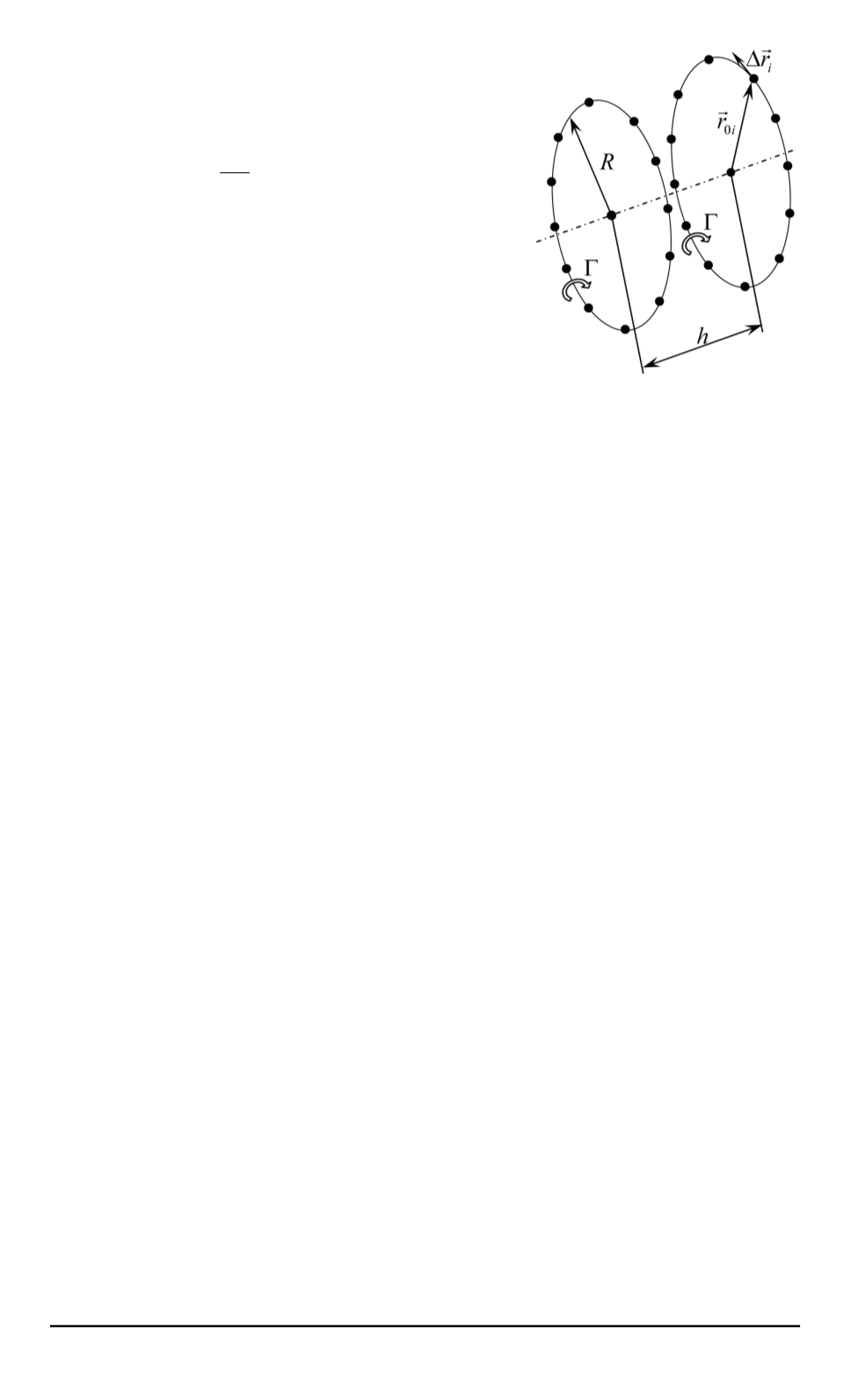
Рис. 2. Вихревые кольца
В качестве метода интегрирования зада-
чи Коши выбран метод Рунге–Кутты второ-
го порядка:
~q
i
=
~q
i
+
~f
(
~q
i
)
Δ
t
2
;
~q
i
+1
=
~q
i
+
~f
(
~q
i
) Δ
t.
Тестирование симметричного ворто-
на.
Вопросы аппроксимации поля завих-
ренности вортонами и индуцированного
ими поля скоростей рассмотрены в рабо-
тах [6, 10]. В данной работе проведено чи-
сленное исследование эволюции завихрен-
ности. Для тестирования предлагаемой рас-
четной схемы выбран известный качествен-
ный эффект “чехарды” двух вихревых колец. Известно [11], что в иде-
альной жидкости такое движение будет периодическим. Нарушение
периодичности в результате численного моделирования позволит су-
дить об адекватности применяемой модели вихревого элемента.
Рассматриваются два тонких вихревых кольца радиусом
R
1
=
R
2
=
=
R
= 1
(рис. 2). В начальный момент времени центры колец лежат
на одной оси, а расстояние между плоскостями колец
h
= 1
,
2
. Цирку-
ляции колец одинаковы и равны
Γ = 1
.
Дискретизация вихревых колец была выполнена, как показано
на рис. 2: каждое вихревое кольцо моделировалось при помощи
N
= 60
симметричных вортонов-отрезков, расставленных равномер-
но по окружности кольца. Радиус дискретности вортонов был выбран
равным
ε
= 0
,
1
, шаг интегрирования по времени
Δ
t
= 0
,
01
.
В результате моделирования получены зависимости радиусов ко-
лец (рис. 3,
а
) и расстояния между кольцами (рис. 3,
б
) от времени. На
рис. 4 приведены зависимости радиусов обоих колец от расстояния
между ними.
Движение колец, как следует из графиков, является периодиче-
ским, что согласуется с теоретическими результатами исследования
“чехарды” вихревых колец в идеальной жидкости [11]. При движении
кольца не выходят из плоскости, сохраняют свою форму и через рав-
ные промежутки времени восстанавливают взаимное расположение в
пространстве. На рис. 5 показаны отдельные фазы половины периода
этого процесса.
Для сравнения проведено аналогичное исследование с использова-
нием сферических вортонов методом core spreading [7]. В этом случае
каждое вихревое кольцо моделировалось при помощи
N
= 360
сфе-
рических вортонов. Для обеспечения устойчивости вычислительного
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4
67


