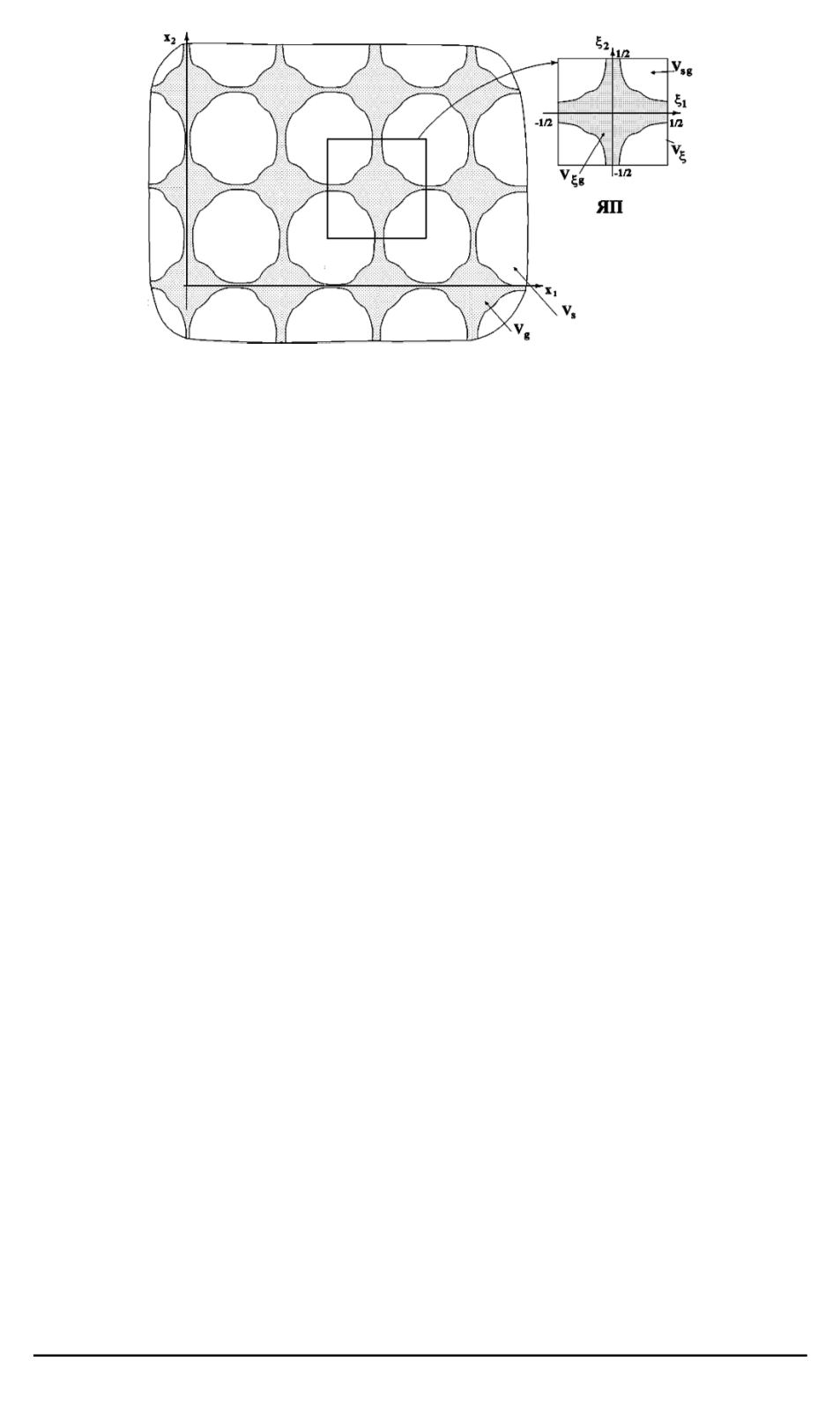
Рис. 1. Пористая периодическая структура с ячейкой периодичности
у которой поры образуют продольные каналы вдоль оси
Oξ
3
. Такая
структура возникает, например, в композиционных однонаправленных
армированных материалах, обладающих продольными порами — тре-
щинами. Выберем в качестве криволинейных координат
X
i
цилиндри-
ческие координаты
X
1
=
r
,
X
2
=
θ
,
X
3
=
z
, в этом случае решение
локальной задачи (1) зависит только от двух координат —
r
и
z
.
В силу линейности локальной задачи (1) ее решение ищем в виде
линейной функции входных данных, т.е. градиента
r
p
(0)
=
p
,
3
e
3
, где
p
,
3
=
∂p/∂
ˉ
x
3
(остальные компоненты градиента
r
p
(0)
в силу однока-
нальной структуры равны нулю, так как отсутствует сквозное течение
по всей пористой структуре по направлениям
Ох
1
и
Ох
2
)
:
p
(1)
=
P
(
r, z
)
p
(0)
,
3
, υ
(0)
r
=
W
r
(
r, z
)
p
(0)
,
3
, υ
(0)
z
=
W
z
(
r, z
)
p
(0)
,
3
.
(2)
Подставляя выражения (2) в локальную задачу (1), после исключе-
ния градиента
r
p
(0)
получаем
r ∙
W = 0;
− r
P
+
μ
Δ
∙
W = e
z
,
в
V
ξg
;
W
(
α
)
= 0
,
на
Σ
ξsg
;
< P >
= 0
,
[ [W] ] = 0
,
[ [
P
] ] = 0
(3)
— локальную задачу для определения давления
P
и вектора скоро-
сти
W =
W
r
e
r
+
W
z
e
z
, где
e
r
,
e
z
,
e
θ
— векторы физического базиса
цилиндрической системы координат
X
i
.
Система (3) представляет собой стационарную задачу течения не-
которой фиктивной линейно-вязкой несжимаемой жидкости. Поло-
жим, что структура ЯП имеет зеркальную симметрию относительно
плоскостей
Oξ
1
ξ
2
и
Oξ
2
ξ
3
, тогда, как было показано в [10], решение
P
,
W
задачи (3) может быть построено с помощью симметричного и
антисимметричного продолжений функций
˜
P
,
˜W
, определенных в 1/4
92
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


