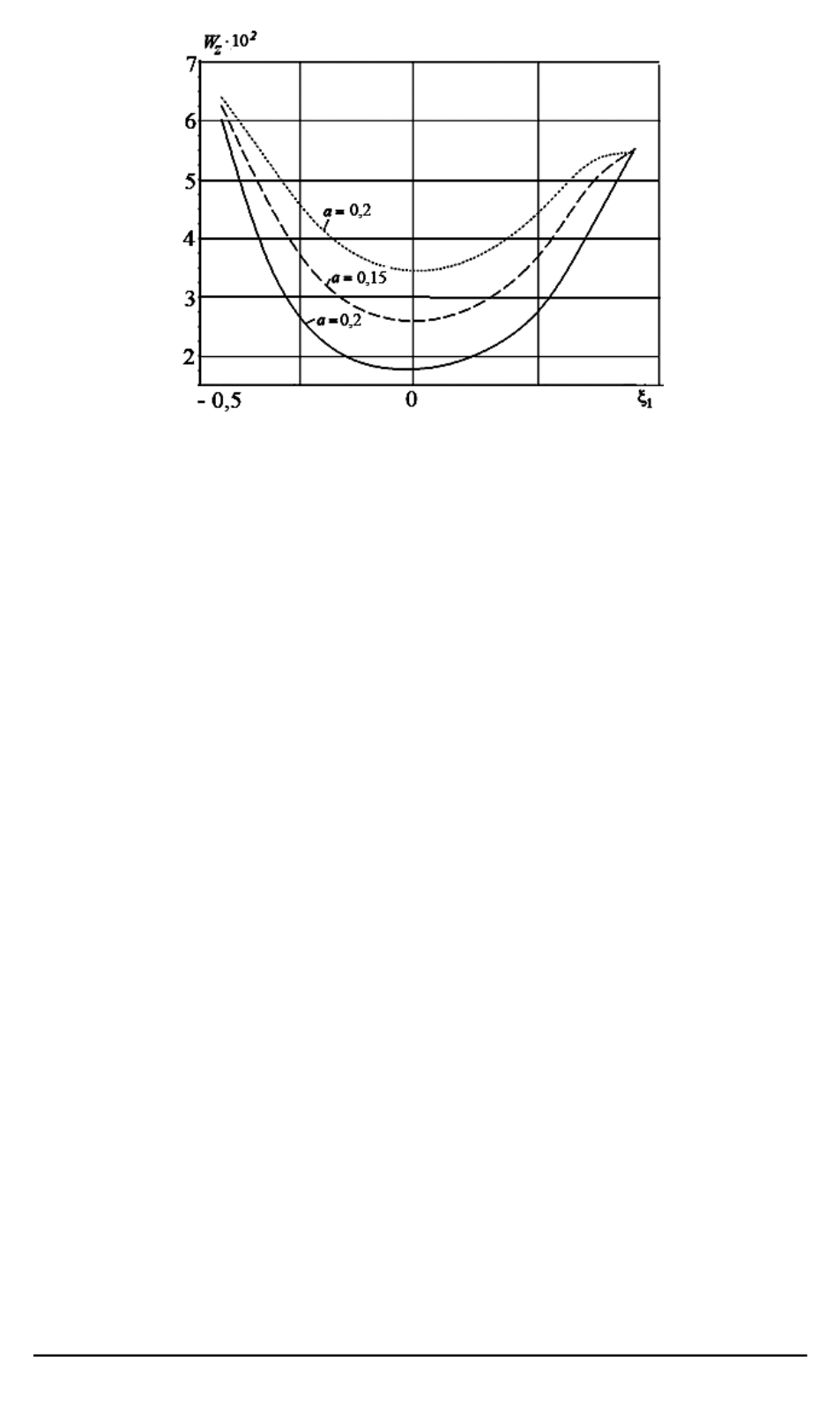
Рис. 3. Распределение проекции скорости
˜
W
z
вдоль продольной оси канала при
различных значениях радиуса входного канала
a
При измельчении регулярной сетки КЭ (т.е. при уменьшении мак-
симальной площади КЭ
S
max
)
, которое приводило к увеличению об-
щего числа КЭ с 200 до 800 и соответственно к увеличению раз-
мерности СЛАУ, было установлено резкое увеличение погрешности
вычислений. В результате абсолютные значения скорости
˜
W
z
возра-
стали примерно на три порядка при использовании метода Гаусса, и
на два — при использовании метода QMR (рис. 4). Кроме того, иска-
жался сам характер решения — появлялся максимум скорости в зоне
максимального сечения поры, противоречащий физическим законам.
Лучшие результаты были получены с применением нерегулярных КЭ
сеток, вычислительная погрешность в этом случае уменьшалась при-
мерно в три раза при использовании метода Гаусcа и в полтора ра-
за при использовании метода QMR (рис. 5). Нефизических максиму-
мов при этом не возникало, а характер распределения скорости
˜
W
z
и других функций был такой же, как и для крупных сеток; число
КЭ для нерегулярной сетки составляло 576 элементов. Практически
полного устранения вычислительной погрешности удалось достичь
при использовании неравномерной КЭ сетки (адаптивной сетки), у
которой происходит сгущение узлов в зоне максимума решения; в
рассматриваемой задаче это зона вблизи оси симметрии канала
Oξ
3
(cм. рис. 5,
г
). При использовании метода QMR для адаптивной сет-
ки погрешность не превышала 10%. Все результаты сравнивались с
решением, полученным конечно-разностным методом функций вихря
и тока, описанным в работе [8]. При использовании адаптивной КЭ
сетки и метода Гаусса погрешность снова возрастала до 10 раз (хотя
характер решения сохранялся правильным и нефизическиe максиму-
98
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3


