сленным значениям четырех коэффициентов
μ
ij
определяются значе-
ния
u
∪
1
,
u
∪
2
в нижнем узле. Значения
u
∪
3
находится из соотношений
(19). Значения
u
j
запоминаются для каждого узла.
Изложенный численный метод позволяет интегрировать систему
нелинейных, взаимосвязанных дифференциальных уравнений и про-
водить расчеты в широком диапазоне изменения параметров набегаю-
щего потока в случае, когда режимы протекания химических реакций
у тела меняются от замороженного до равновесного.
Расчеты выполнены для осесимметричного тела с радиусом сфе-
рического затупления
R
m
= 0
,
8
∙
10
−
2
м при числе Маха M
∞
= 22
. Па-
раметры набегающего потока выбраны для высоты полета
H
= 60
км.
В соответствии со значениями параметров набегающего потока, па-
раметры на внешней границе пограничного слоя имеют значения:
T
δ
= 6100
K,
c
N
2
= 0
,
4097
,
c
O
2
= 0
,
2702
∙
10
−
4
,
c
NO
= 0
,
1254
∙
10
−
1
,
c
N
= 0
,
3469
,
c
O
= 0
,
2308
,
c
N
= 0
,
77
[1, 2, 6]. На стенке заданы сле-
дующие условия:
T
w
= 290
K,
c
r
0
= 0
(
r
=
N,O,NO),
c
N0
= 0
,
77
. Тол-
щина пограничного слоя в критической точке
δ
= 6
мм,
V
s
= 180
м/с,
Pr
= 0
,
71
, Sc
i
=
Sc
N
= 0
,
65
,
μ
≈
T
0
,
77
. Энтальпия на границе погра-
ничного слоя
h
δ
= 0
,
235
∙
10
8
м
2
/с
2
, давление
p
δ
= 10133
Па. Набегаю-
щий поток — диссоциированный воздух, вдуваемый газ — воздух при
k
w
N
= 0
,
k
w
O
= 2
м/c (рис. 2–5).
Обсуждение результатов.
В результате численного решения по-
лучены зависимости теплового потока от интенсивности вдува (см.
рис. 2) в критической точке и распределения концентраций N
2
, O
2
, N,
NO по толщине пограничного слоя в зависимости от параметра вдува
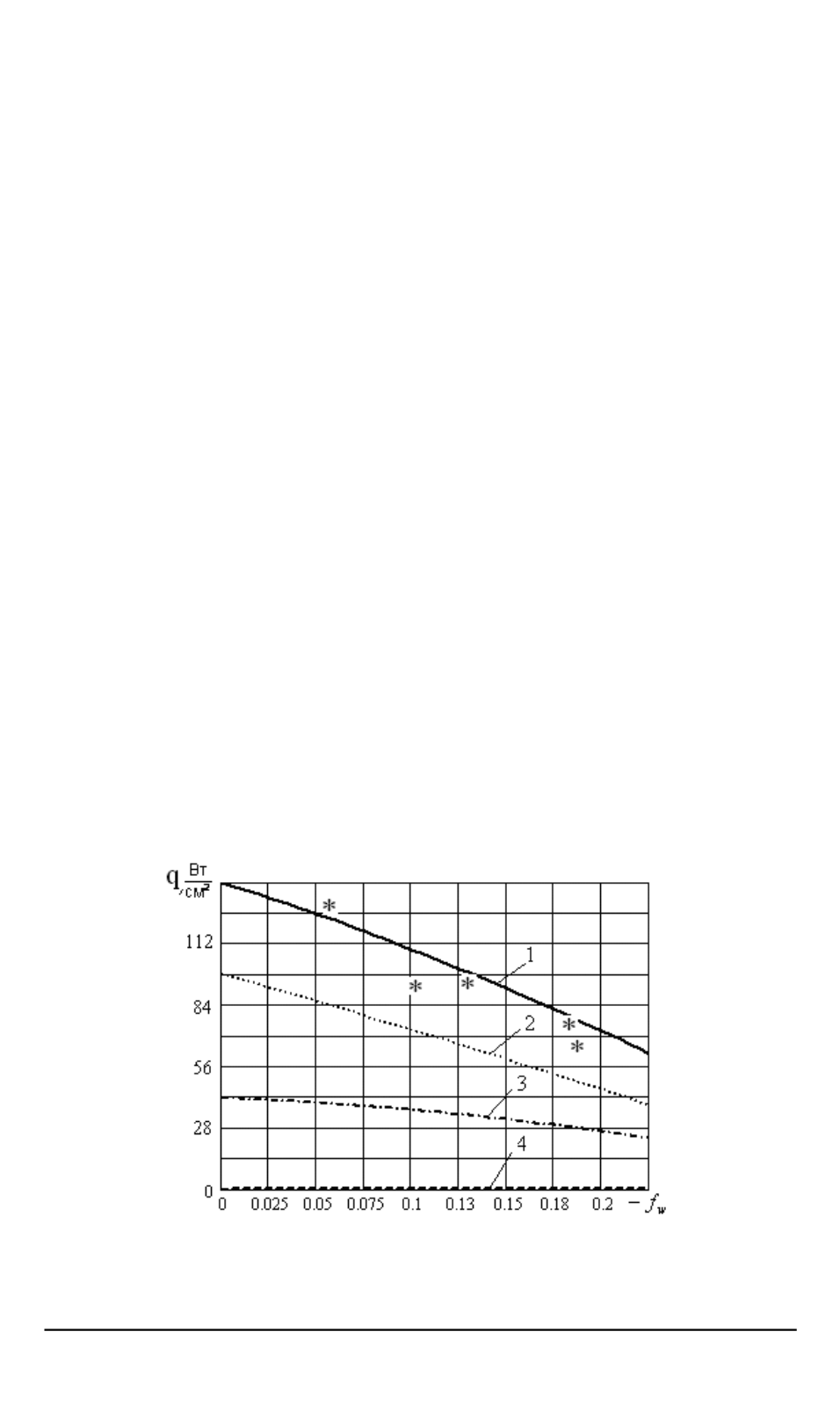
Рис. 2. Зависимость теплового потока от интенсивности вдува:
1
— суммарный тепловой поток к поверхности;
2
,
3
и
4
— составляющие теплового
потока, обусловленные теплопроводностью и диффузией атомов азота и кислорода
50
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


