Поскольку
Ξ
i
=
−
dξ
i
dξ
Ξ
,
то
Ξ
≡
0
.
Таким образом, мы получили
особенный случай
. Результаты числен-
ного моделирования приведены на рис. 1.
Проведя аналогичные выкладки для случаев
Δ
2
= 0
и
Δ
3
= 0
, не-
трудно увидеть, что и при этих условиях получаем
особенный случай
.
Таким образом, система (1) с одним нулевым корнем и двумя с отрица-
тельными действительными корнями характеристического уравнения
устойчива, но не асимптотически.
Рассмотрим теперь случай
a
=
b
. При этом система (2) имеет два
одинаковых корня:
x
1
=
x
2
=
1
−
ar
−
2
a
2
+
a
+ 1
, x
3
=
r
(
a
+ 1)
−
2
a
−
2
a
2
+
a
+ 1
.
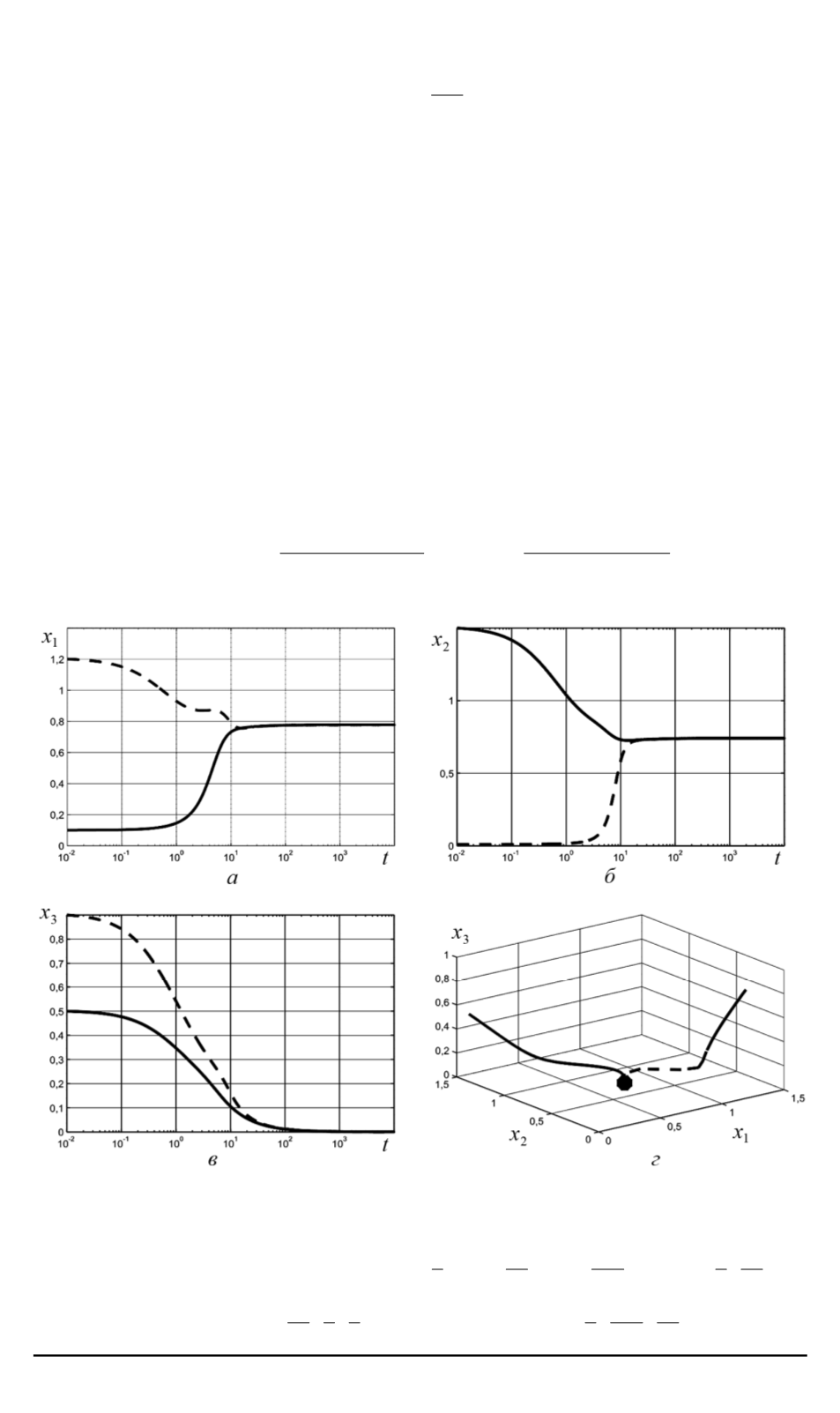
Рис. 1. Зависимость численности первой (
а
), второй (
б
) и третьей (
в
) популяций
от времени; фазовый график численности популяций (
г
):
параметры интегрирования:
x
3
= 0
,
a
=
1
3
,
b
=
3
10
,
r
=
389
810
,
x
=
7
9
,
20
27
,
0
;
сплошная кривая —
x
0
1
=
1
10
,
3
2
,
1
2
; штриховая —
x
0
2
=
6
5
,
1
100
,
9
10
66
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4


