Частные случаи.
Рассмотрим несколько частных случаев, для ко-
торых удалось построить графически области, в которых имеет место
тот или иной тип удара.
Стопы ног расположены симметрично относительно центра
масс
(
b
1
=
b
2
=
b
). Введем безразмерные параметры
˜
ρ
=
ρ/b
,
˜
h
=
h/b
. В силу утверждения 1 после удара тело останавливается,
если
˜
h
≤
p
1
−
˜
ρ
2
и
f
≥
˜
h
; скользит на двух ногах, если
˜
h
≤
p
1
−
˜
ρ
2
и
f <
˜
h
, либо
˜
h >
p
1
−
˜
ρ
2
и
f
≤
F
; скользит на стопе
S
2
и враща-
ется вокруг нее, если
˜
h >
p
1
−
˜
ρ
2
и
F < f <
Φ
; вращается вокруг
неподвижной стопы
S
2
, если
˜
h >
p
1
−
˜
ρ
2
и
f
≥
Φ
. Здесь
F
( ˜
h
) = (1
−
˜
ρ
2
)
/
˜
h,
Φ( ˜
h
) = ˜
h/
(˜
ρ
2
+ ˜
h
2
)
.
Функция
Φ( ˜
h
)
имеет локальный максимум в точке
˜
h
= ˜
ρ
, точку
перегиба при
˜
h
=
√
3˜
ρ
и
Φ
˜
h
=0
= 0
,
Φ
˜
h
=
√
1
−
˜
ρ
2
=
p
1
−
˜
ρ
2
,
max
˜
h
Φ = Φ
˜
h
=˜
ρ
=
1
2˜
ρ
,
lim
˜
h
→∞
Φ = 0
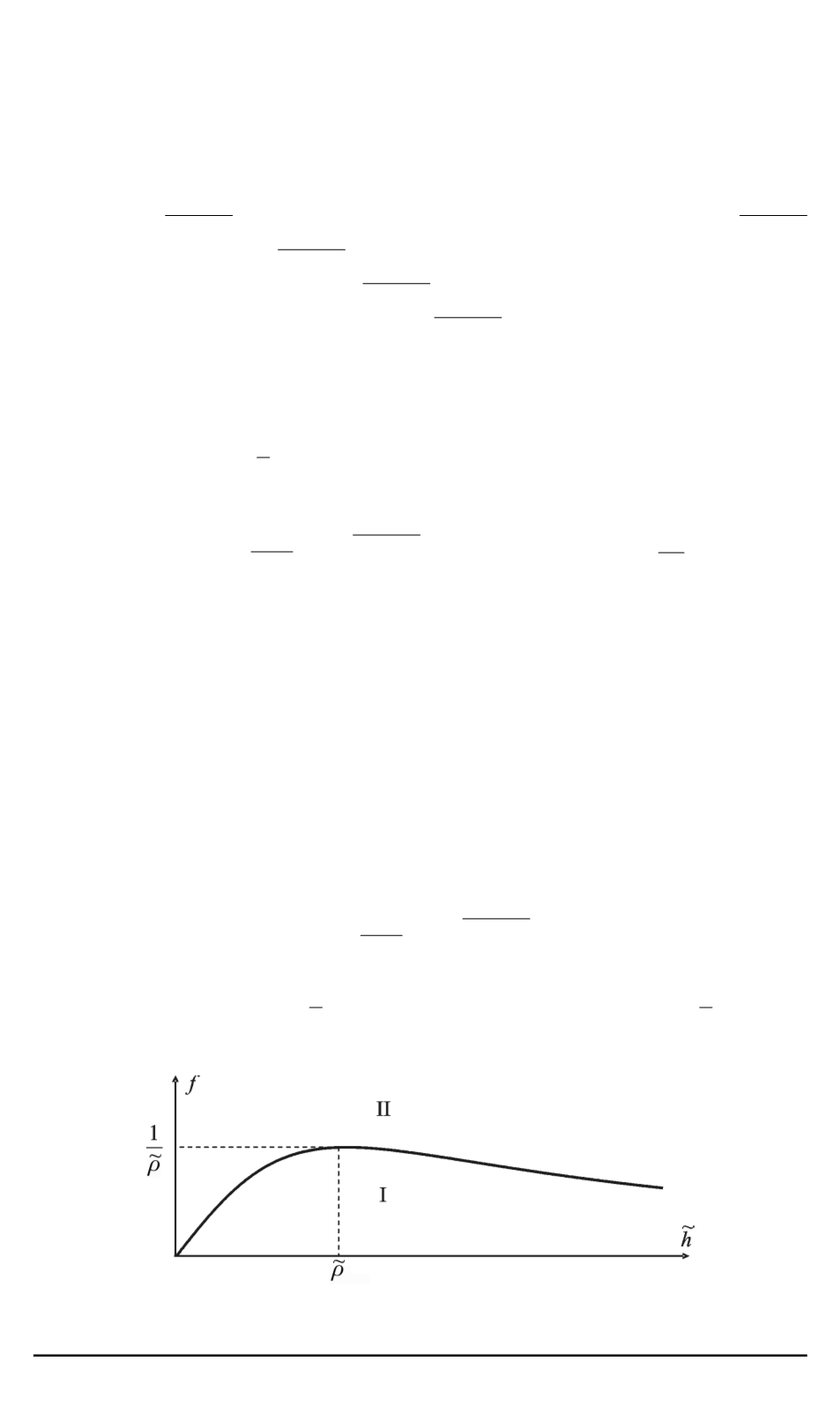
График функции
Φ( ˜
h
)
показан на рис. 2.
Если
˜
ρ
≥
1
, то функция
F
( ˜
h
)
≤
0
и
δ
≥
0
, причем
δ
= 0
только при
˜
h
= 0
. Следовательно, удар двумя ногами с последующим остановом
тела или скольжением на двух ногах невозможны. Функция
Φ( ˜
h
)
делит
множество допустимых значений параметров
˜
h
≥
0
и
f
≥
0
на две
области (рис. 2). В области I после удара тело скользит на стопе
S
2
и
вращается вокруг нее, а в области II — вращается вокруг неподвижной
стопы
S
2
.
Если
˜
ρ <
1
, то функция
F
( ˜
h
)
является монотонно убывающей
гиперболой и
F
( ˜
h
)
>
0
, F
˜
h
=
√
1
−
˜
ρ
2
=
p
1
−
˜
ρ
2
,
lim
˜
h
→∞
F
= 0
.
Возможны все четыре типа удара. Графические изображения отли-
чаются для случаев
1
/
√
2
≤
˜
ρ <
1
(рис. 3) и
0
<
˜
ρ <
1
/
√
2
(рис. 4).
Рис. 2. Области, соответствующие различным типам удара. Случай симметрич-
ного расположения стоп, радиус инерции
˜
ρ >
1
48
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2


