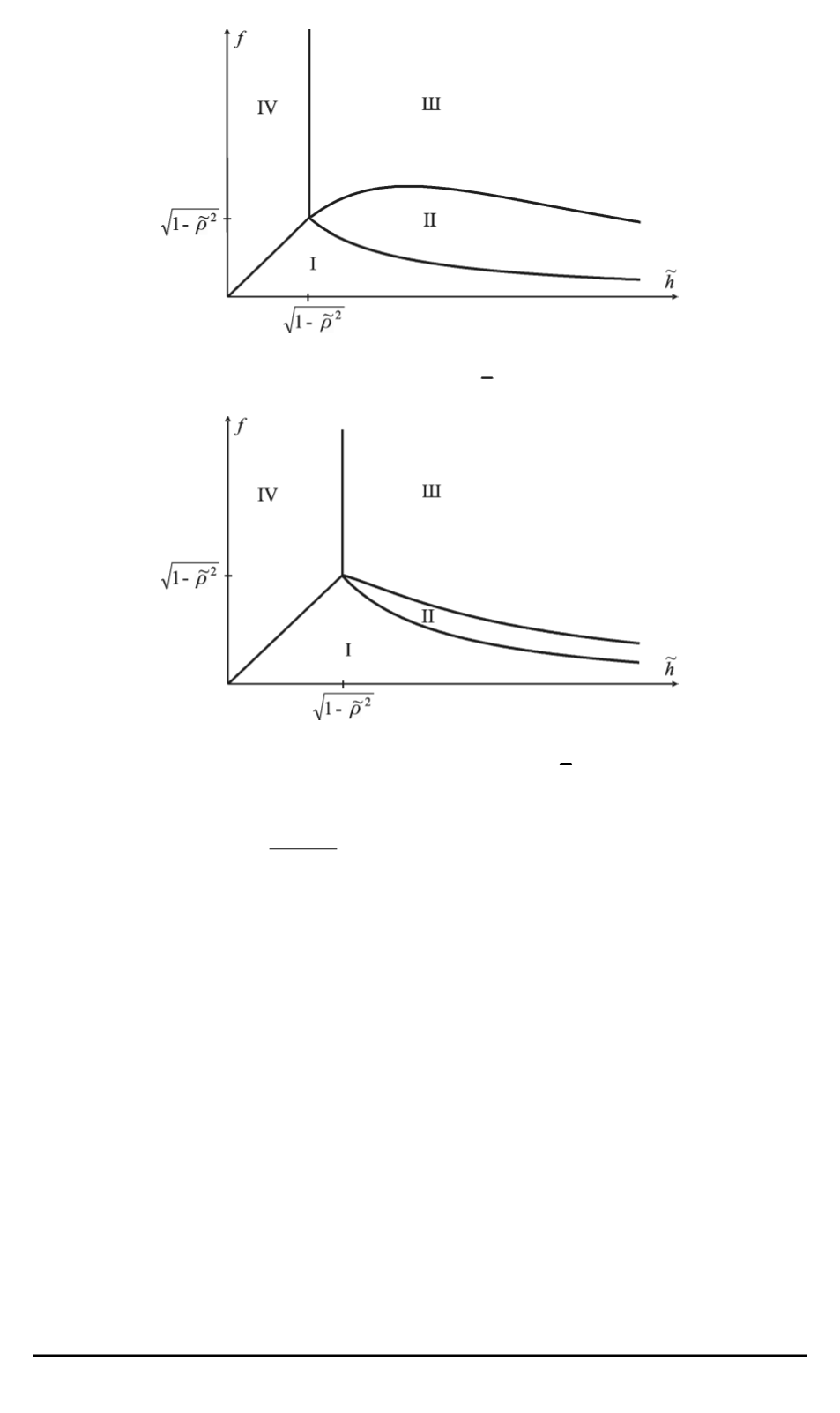
Рис. 3. Области, соответствующие различным типам удара. Случай симметрич-
ного расположения стоп, радиус инерции
1
/
√
2
≤
˜
ρ <
1
Рис. 4. Области, соответствующие различным типам удара. Случай симметрич-
ного расположения стоп, радиус инерции
0
≤
˜
ρ <
1
/
√
2
В первом случае максимум функции
Φ( ˜
h
)
лежит справа от точки би-
фуркации
˜
h
=
f
=
p
1
−
˜
ρ
2
, а втором случае — слева от нее и поэтому
он отсутствует на границе, разделяющей области I и II. В области I по-
сле удара тело скользит на двух ногах, в области II скользит на стопе
S
2
и вращается вокруг нее, в области III вращается вокруг неподвижной
стопы
S
2
, в области IV останавливается.
В этих случаях решение задачи является корректным с точки зре-
ния непрерывной зависимости решения от параметров. На границах
пределы каждой из этих областей совпадают, и решение можно опре-
делять по любой из формул, соответствующих граничным областям,
а в точке бифуркации — по формулам, соответствующим любому из
четырех случаев.
Если тело является материальной точкой
˜
ρ
= 0
(рис. 5), то
Φ( ˜
h
) =
=
F
( ˜
h
)
. Становится невозможным случай скольжения на стопе
S
2
c
вращением вокруг нее, что ранее отмечалось в работе [4]. На рис. 5 в
области I после удара тело скользит на двух ногах, в области II враща-
ется вокруг неподвижной стопы
S
2
, в области III останавливается. При
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2
49


