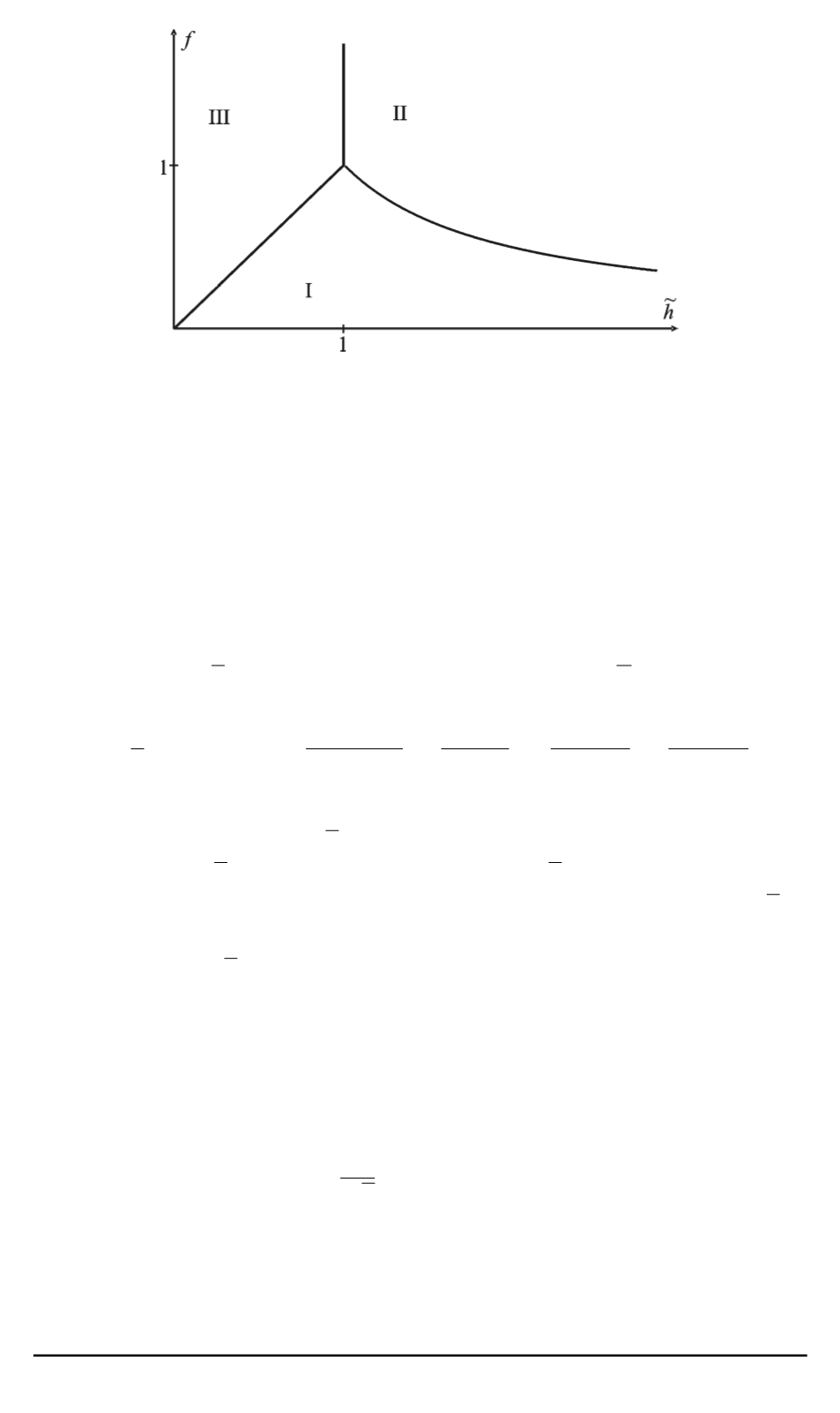
Рис. 5. Области, соответствующие различным типам удара для материальной
точки с симметричным расположением стоп
этом решение задачи становится некорректным — на границе областей
I и II решение меняется скачкообразно.
Однородная прямоугольная пластина
на ножках, размерами кото-
рых можно пренебречь;
2
b
— ширина пластины,
2
a
— высота. Введем
безразмерный параметр
˜
a
=
a/b
, тогда
ρ
2
=
1
3
(
a
2
+
b
2
)
, h
=
a, b
1
=
b
2
=
b,
h
b
= ˜
a,
δ
=
2
3
b
2
(2˜
a
2
−
1)
,
b
1
b
2
−
ρ
2
b
1
h
=
2
−
˜
a
2
3˜
a
,
b
2
h
ρ
2
+
h
2
=
3˜
a
4˜
a
2
+ 1
.
В силу основного утверждения после удара тело останавлива-
ется, если
0
≤
˜
a
≤
1
/
√
2
и
f
≥
˜
a
; скользит на двух ногах, если
0
≤
˜
a
≤
1
/
√
2
и
f <
˜
a
либо
˜
a >
1
/
√
2
и
f
≤
(2
−
˜
a
2
)
/
3˜
a
;
скользит на стопе
S
2
и вращается вокруг нее, если
˜
a >
1
/
√
2
и
(2
−
˜
a
2
)
/
3˜
a < f <
3˜
a/
(4˜
a
2
+1)
; вращается вокруг неподвижной стопы
S
2
, если
˜
a >
1
/
√
2
и
f
≥
3˜
a/
(4˜
a
2
+ 1)
.
На плоскости безразмерных параметров
˜
a
— отношение высоты
пластины к ее ширине,
f
— коэффициент трения — (рис. 6), и в обла-
сти I после удара тело скользит на двух ногах, в области II скользит на
стопе
S
2
и вращается вокруг нее, в области III вращается вокруг непо-
движной стопы
S
2
, в области IV останавливается. Точка бифуркации
имеет координаты
˜
a
=
f
=
1
√
2
.
Циркуль.
Рассмотрим тело, состоящее из двух одинаковых одно-
родных стержней, скрепленных за концы под углом
2
α
(рис. 7). Масса
каждого стержня равна
m
, длина
2
l
. Центр масс тела расположен в
точке
C
, причем
C
1
C
=
C
2
C
,
OC
1
=
OC
2
=
C
1
S
1
=
C
2
S
2
=
l
. Удар
50
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2


