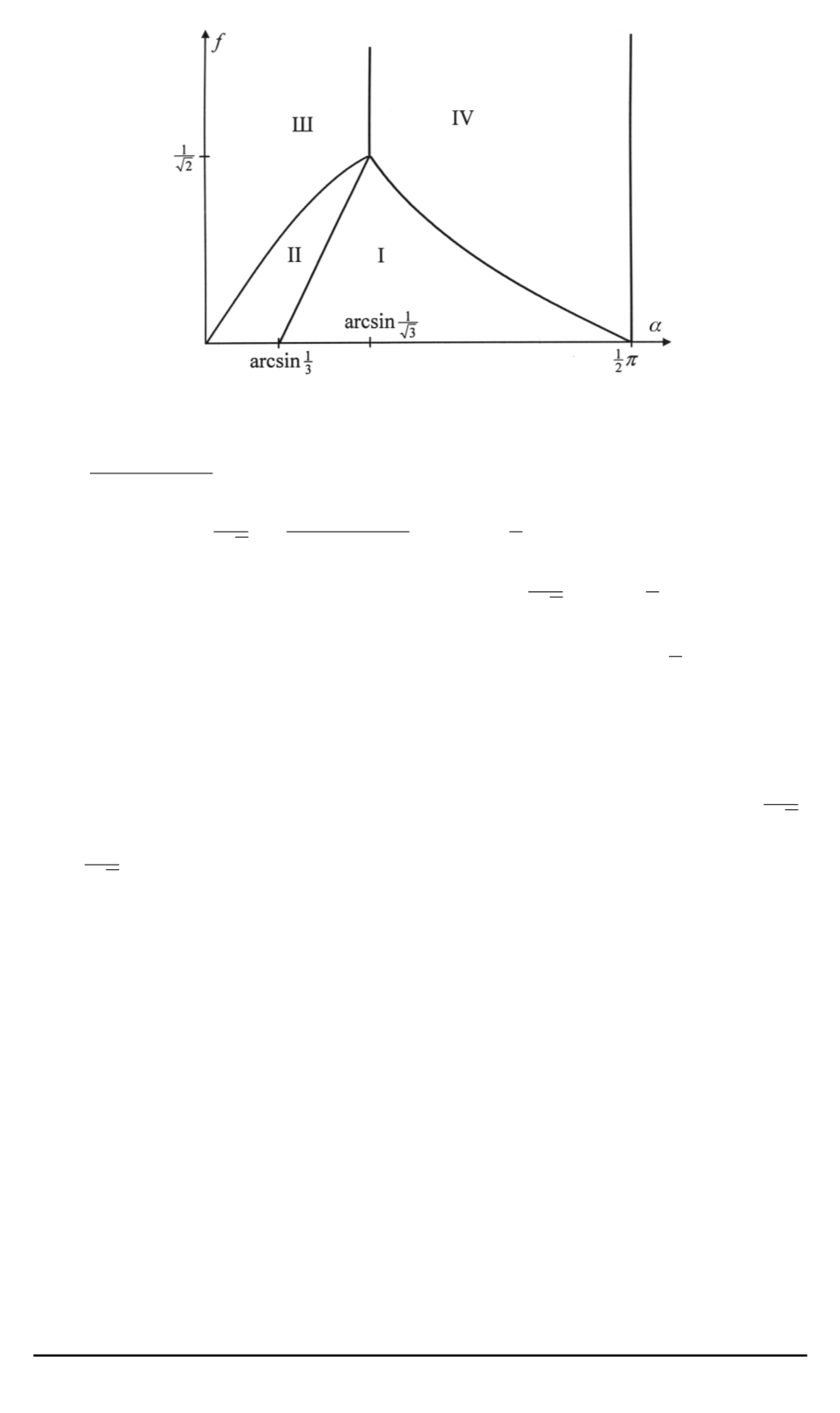
Рис. 8. Области, соответствующие различным типам удара для циркуля
f
≤
9 sin
2
α
−
1
3 sin 2
α
; скользит на стопе
S
2
и вращается вокруг нее, если
0
≤
α <
arcsin
1
√
3
и
9 sin
2
α
−
1
3 sin 2
α
< f <
3
4
sin 2
α
; вращается вокруг
неподвижной стопы
S
2
, если
0
≤
α <
arcsin
1
√
3
и
f
≥
3
4
sin 2
α
.
На плоскости безразмерных параметров угол
α
2
0
,
1
2
π
,
f
— ко-
эффициент трения (рис. 8), и в области I после удара тело скользит на
двух ногах, в области II скользит на стопе
S
2
и вращается вокруг нее,
в области III вращается вокруг неподвижной стопы
S
2
, в области IV
останавливается. Точка бифуркации имеет координаты
α
= arcsin
1
√
3
,
f
=
1
√
2
.
СПИСОК ЛИТЕРАТУРЫ
1. Ф о р м а л ь с к и й А. М. Перемещение антропоморфных механизмов. – М.:
Наука, 1982.
2. Ф о р м а л ь с к и й А. М., Ш е в а л ь р о К., П е р р а Б. Об ударном
взаимодействии тела с опорой // Вестник Московского ун-та. Сер. “Математика,
механика”. – 2000. – № 1. – C. 27–32.
3. Л а п ш и н В. В. Экстренный останов шагающей машины на абсолютно
шероховатой поверхности // Препринт Ин-та прикл. мат. РАН. – 1996. – № 85.
4. L a p s h i n V. Model problem of a walking machine emergency stop // 5th IFAC
Symposium on Robot Control, Vol. 3, Nantes, France, 1997. – P. 807–812.
5. О х о ц и м с к и й Д. Е., Г о л у б е в Ю. Ф. Механика и управление
движением автоматического шагающего аппарата. – М.: Наука, 1984.
6. П л я в н и е к с В. Ю. Расчет косого удара о препятствие // Вопросы динамики
и прочности. – Рига: Зинатне, 1969. – № 18. – C. 87–109.
52
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2


