При
¯
A
= ¯
B
= 0
из соотношений
(25), (26)
следуют формулы перво
-
го приближения ТКВ для
∆
p
2
и
τ
[4].
Из соотношений
(25), (26)
также
видно
,
что на большом удалении от начального сечения
(
∆¯
p
2
→
0
)
при
использовании первого и второго приближений ТКВ можно получить
одинаковые результаты
.
Вычисления по формулам
(25), (26)
для первого и второго прибли
-
жений ТКВ сравнивались с результатами численного решения задачи о
распространении плоской УВ
,
заданной в начальном сечении треуголь
-
ной эпюрой избыточного давления
(20),
в совершенном газе с показа
-
телем адиабаты
k
= 1
,
4
(
для воздуха
)
при различных значениях
∆¯
p
0
2
(
аналогично работе
[4]).
На рис
. 3
представлены результаты такого сравнения для
∆¯
p
0
2
= 0
,
2
.
С использованием первого приближения получены заниженные зна
-
чения
∆
p
2
при любых расстояниях
.
Максимальная относительная по
-
грешность наблюдается при
¯
x
≈
20
и достигает
8,5 %,
а при
¯
x
= 130
она снижается до
6,7 %.
С использованием второго приближения по
-
лучены незначительно завышенные значения избыточного давления на
фронте при малом удалении от начального сечения
(
в пределах
1 %
при
¯
x <
20
)
и несколько заниженные значения
∆
p
2
на большом удалении
(
занижение достигает
2 %
при
¯
x
= 130
).
При увеличении избыточного
давления на фронте УВ в начальном сечении до значения
∆¯
p
0
2
= 0
,
25
ошибки вычислений
∆
p
2
с использованием первого приближения воз
-
растают в ближней области до
10 %,
а при
¯
x
= 130
становятся больше
7 %.
С использованием второго приближения получены завышенные
значения
∆
p
2
в ближней зоне в пределах
3 %,
а при
x
= 130
—
зани
-
женные менее чем на
2 %.
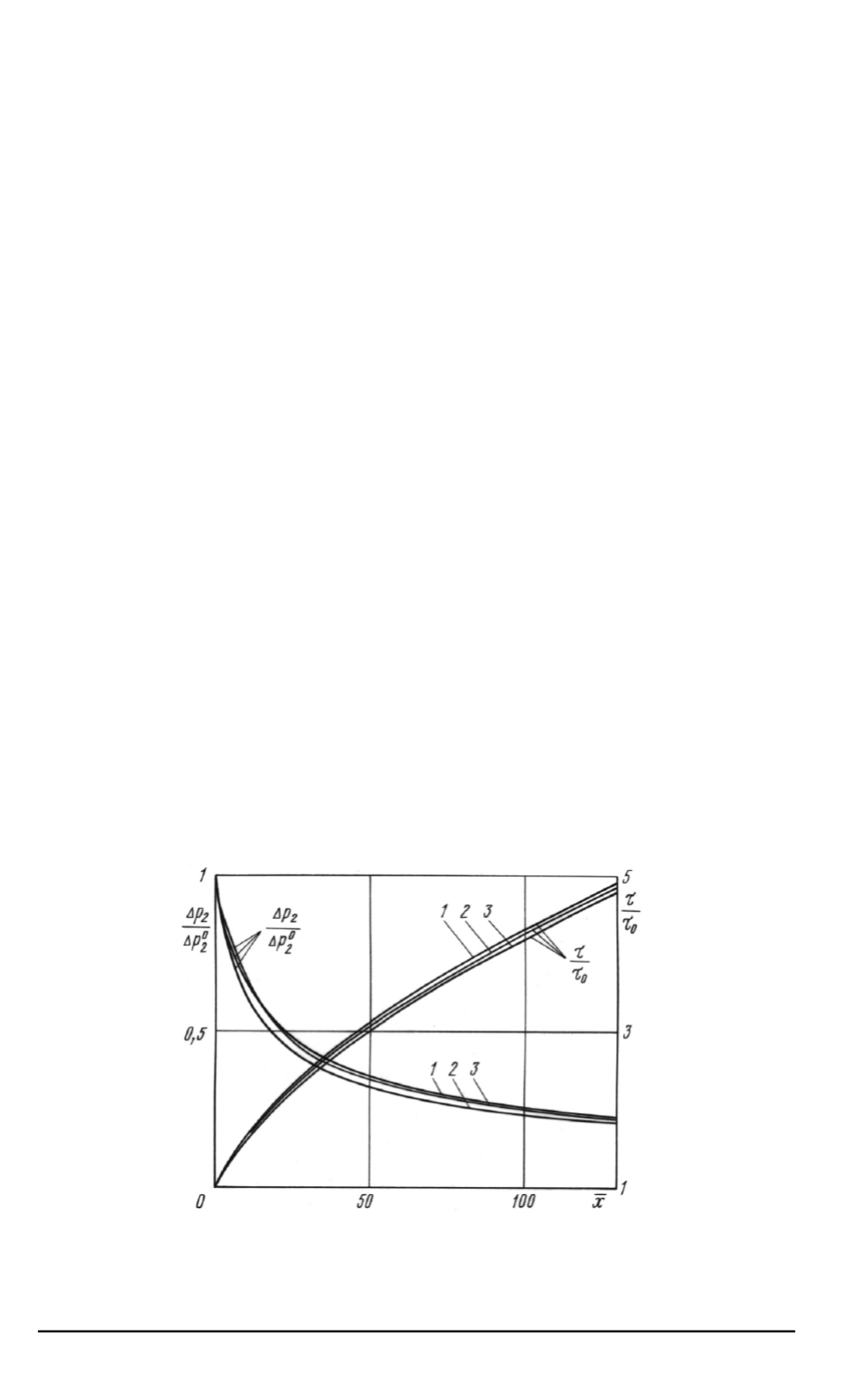
Рис
. 3.
Сравнение результатов
,
полученных с использованием первого и второго
приближений
:
1
—
точное значение
;
2
—
первое приближение
;
3
—
второе приближение
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
65


