Формирование устойчивых электромагнитных образований в ограниченных пространственных структурах, обладающих аксиальной симметрией - page 13

На основе разработанной компьютерной программы была проведе- на оптимизация числа проходов ОД при выбранном p 2 (4 , 10) и рас- считаны смещения ИК для оптимальных траекторий при прохождении
лучей в оптическом диске в одном направлении (табл. 2). В расчетах
были использованы следующие параметры: R0 = 0, 06 м, ω = 630 рад/ с,
λ = 0 ,6328 мкм, n2 = 1, 5.
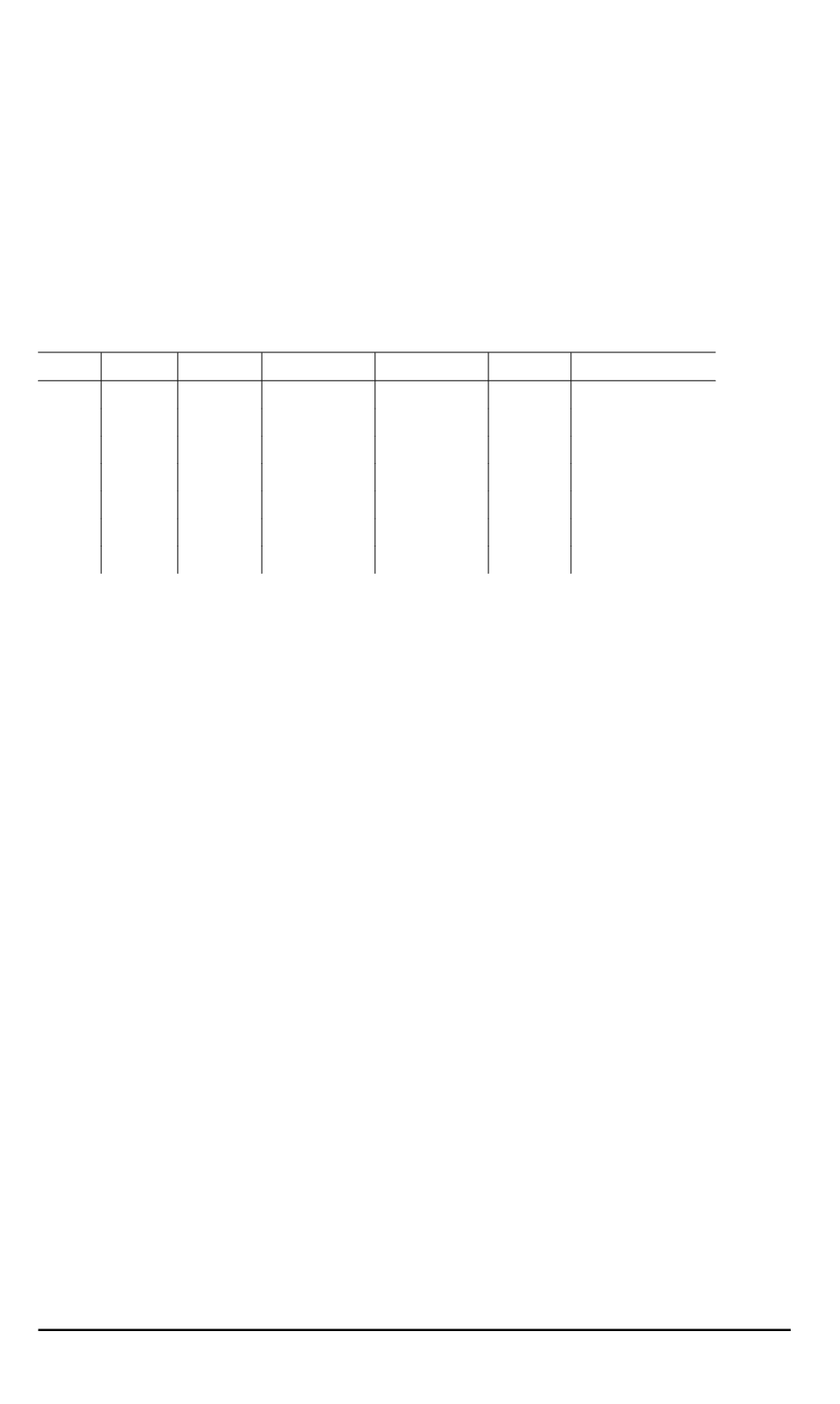
Таблица 2
Результаты расчетов разности хода интерферирующих лучей приоптимизации числа проходов в ОД
p kopt mopt ϑ0 , град ϑ2 , град Nopt ΔLe, м
4 2 2 0 0 2 0
5 2 1 27,6 18 5 1,07 ∙ 10−7
6 2 2 48,6 30 3 7,01 ∙ 10−8
7 3 1 19,5 13 7 1,18 ∙ 10−7
8 3 1 35,0 22 8 1,91 ∙ 10−7
9 4 1 15,1 10 9 1,22 ∙ 10−7
10 3 1 61,8 36 10 1,79 ∙ 10−7
Для каждого отдельного числа разбиений p в табл. 2 представлены
данные оптимальной замкнутой траектории. Для p = 8 имеем угол
ϑ0 = 35◦ , причем он близок к значению ϑeff
0 ≈ 41◦. При этом число про- ходов Nopt равно восьми и величина накопленной разности хода мак- симальна: ΔLe = 1,91 ∙ 10−7 м (0,3 полосы). Для p = 10 имеем угол
ϑ0 = 61,8◦ , который сильно отличается от ϑeff
0 . При этом число прохо- дов Nopt равно десяти , что несколько больше, чем для p = 8, но разность
хода ΔLe = 1,79 ∙ 10−7 м (0,27 полосы) меньше , чем в предыдущем слу- чае. Данный пример иллюстрирует тот факт, что при увеличении числа
проходов накопленный лучом сдвиг фазы вследствие вращения диска
не всегда максимален. Поэтому предложенная процедура оптимизации
числа переотражений должна применяться на этапе разработки опти- ческой схемы интерферометра. Оптическая схема интерферометра с переотражением луча на ци- линдрической поверхности может иметь более высокую чувствитель- ность по сравнению со схемой интерферометра , представленной в ра- боте [17], из-за возможности создания большого числа переотражений. Это может быть использовано для проверки решения дисперсионного
уравнения в трехмерном случае движения среды и для исследования
пространственного увлечения света в среде со сложным движением. Поскольку решение дисперсионного уравнения имеет нелинейный вид, обсуждаемая схема интерферометра позволит экспериментально про- верить неинвариантные свойства преобразований частных дифферен- циалов пространства и времени. Заметим также, что диаграмма k( p)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2005. № 2 15