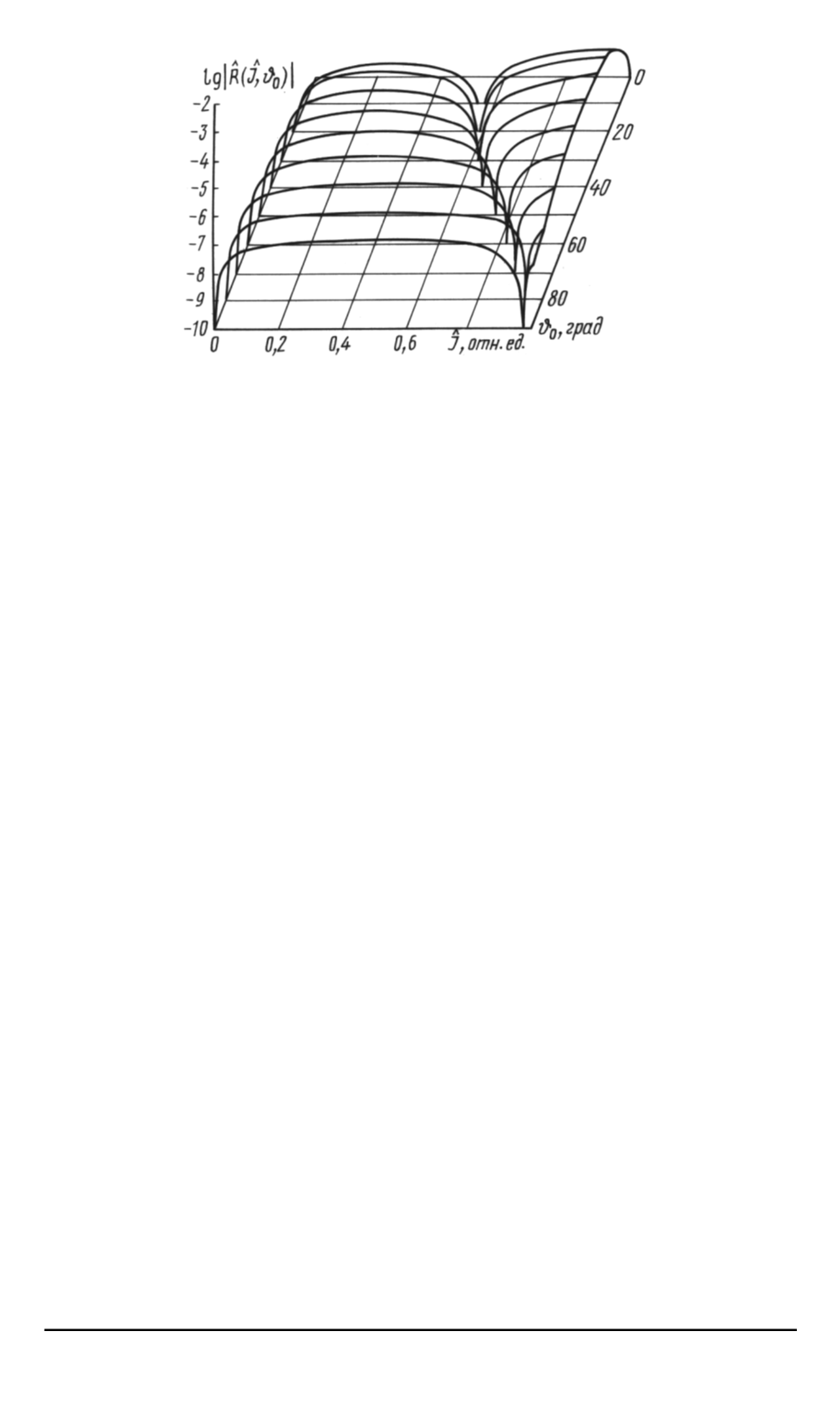
Рис
. 3.
Зависимость кратчайшего расстояния
ˆ
R
от траектории волнового векто
-
ра электромагнитной волны до прямой
,
по которой распространяется свет при
ω
= 0
,
от угла падения
ϑ
0
и нормированной длины пути
ˆ
J
где
ϑ
0
2
—
угол преломления при
ω
= 0
.
Решение интегрального уравнения представлено на рис
. 3
для сле
-
дующих параметров
:
k
0
= 10
−
7
м
−
1
,
n
1
= 1
,
n
2
= 1
,
5
,
R
0
= 0
,
1
м
,
ω
= 10
4
рад
/c.
Как следует из графиков
,
величина
ˆ
R
возрастает от
ˆ
R
= 0
при
ϑ
0
2
= 0
◦
до
ˆ
R
≈
10
−
7
м при
ϑ
0
2
= 90
◦
.
Зависимость
ˆ
R
( ˆ
J, ϑ
0
)
приведена
по модулю
,
поэтому график делится на две части
:
до пересечения с
прямой траекторией
,
где
ˆ
R >
0
,
и после пересечения
,
где
ˆ
R <
0
.
Введем дополнительные параметры
:
p
—
число разбиений окружно
-
сти
,
образующей цилиндрическую поверхность диска
,
k
—
число про
-
пусков делений окружности между соседними переотражениями
,
N
—
число проходов луча до попадания в исходную точку ОД
.
Пусть
m
—
наибольший общий делитель чисел
p
и
k
;
тогда спра
-
ведливо равенство
N
=
p/m
.
Пусть
,
например
,
p
= 9
и
k
= 3
;
тогда
N
= 3
,
что указывает на образование замкнутой траектории при срав
-
нительно малом числе переотражений
(
рис
. 4).
В случае
,
когда
p
= 9
и
k
= 4
,
получим
N
= 9
и смещение интерференционной картины бу
-
дет существенно больше
.
Однако не все замкнутые траектории
,
кото
-
рые можно изобразить геометрически
,
реализуемы в оптическом диске
при вводе светового луча через цилиндрическую поверхность диска
.
Так
,
при
p
= 9
,
k
= 2
,
N
= 9
преломленный луч должен иметь угол
преломления
ϑ
2
= 50
◦
.
Вместе с тем
,
при вводе луча из среды с показа
-
телем преломления
n
1
= 1
в среду ОД с показателем
n
2
= 1
,
5
для угла
ϑ
2
= 50
◦
не существует угла падения
ϑ
0
.
Численные расчеты показывают
,
что зависимость накопленной
оптической разности хода лучей
Δ
L
e
,
прошедших вращающийся ОД
в противоположных направлениях
,
от угла падения
ϑ
0
имеет макси
-
10
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2


