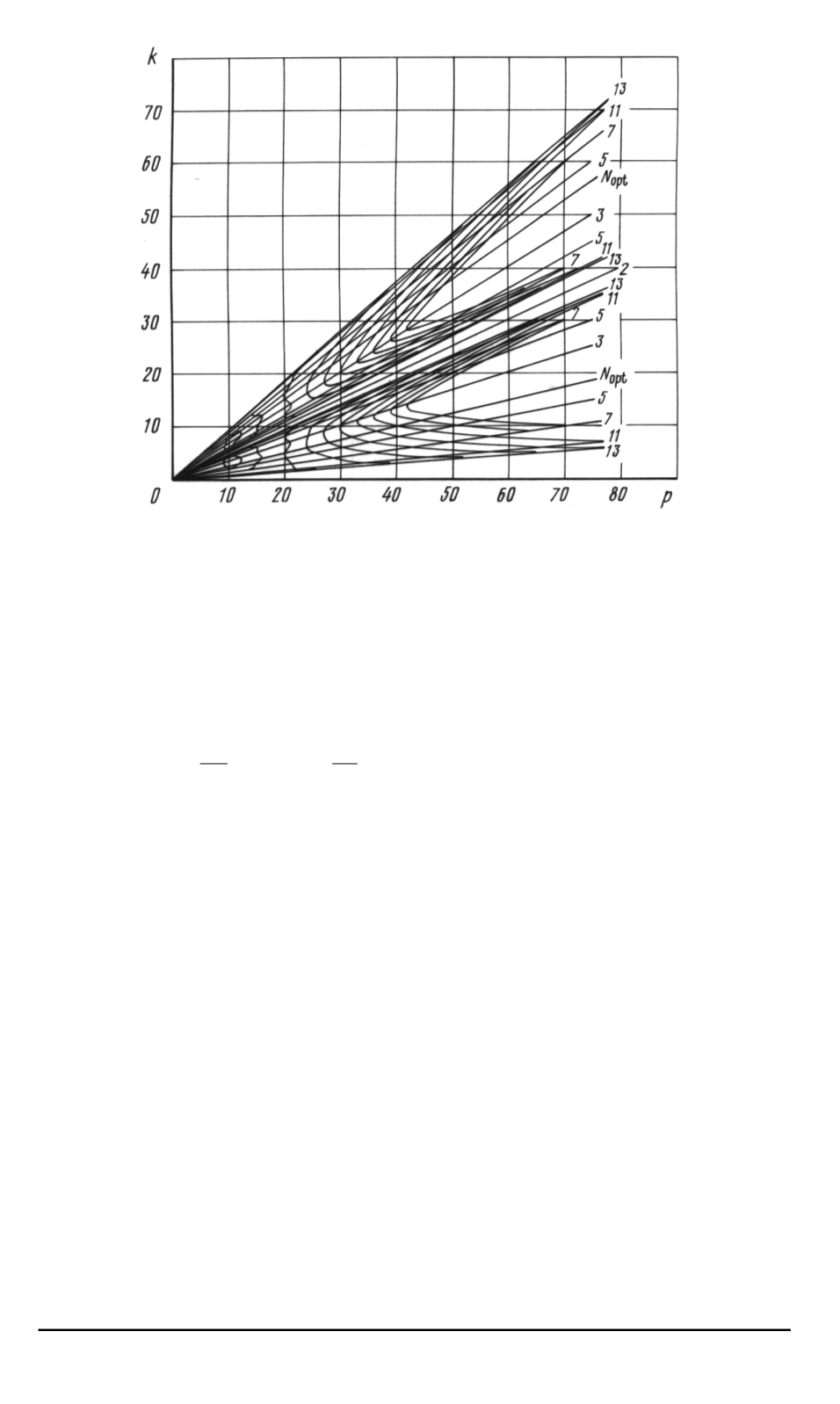
Рис
. 5.
Распределение простых чисел
N
= 3
,
5
,
7
,
11
,
13
отражения луча в зависи
-
мости от числа
p
разбиения окружности на равные части и числа
k
пропусков
делений между соседними переотражениями
Перейдем в формуле
(7)
к углу падения
ϑ
0
и учтем четность функ
-
ции
.
Тогда получим два решения
:
tg
ϕ
1
=
1
2
π
arccos 2
n
2
1
n
2
2
sin
2
ϑ
0
−
1
,
tg
ϕ
2
= 1
−
tg
ϕ
1
,
(8)
которые соответствуют возможности симметричного ввода луча в ОД
(
первое решение для случая
,
когда
k < p/
2
,
второе решение
—
для
k > p/
2
).
Рассмотрим случай
n
1
= 1
,
n
2
= 1
,
5
(
оптическое стекло
“
крон
”),
ϑ
eff
0
≈
41
◦
.
Тогда из соотношений
(7), (8)
получим
:
k
1
= 89
,
p
= 250
,
N
= 250
при
ϕ
1
= 19
,
59
◦
;
k
2
= 161
,
p
= 250
,
N
= 250
при
ϕ
2
= 32
,
785
◦
.
Заметим
,
что
k
1
+
k
2
=
p
.
Прямые
,
соответствующие углам
ϕ
1
и
ϕ
2
,
изображены на диаграмме
,
представленной на рис
. 5.
Интересно
,
что прямые проходят вблизи вершин семейств кривых
,
соответствующих простым числам на диаграмме
.
Представление результатов на диаграмме позволяет достаточно лег
-
ко оценить оптимальные значения
N
и
k
путем нахождения максималь
-
ного значения
N
в точках диаграммы вблизи прямой
,
проходящей под
углом
ϕ
1
= 19
,
59
◦
,
для значений
p
2
(
N
min
, N
max
)
.
В случае
,
если в этом
диапазоне значений
p
все числа
N
i
меньше
N
min
,
проверяют область
р
> N
max
.
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
13


