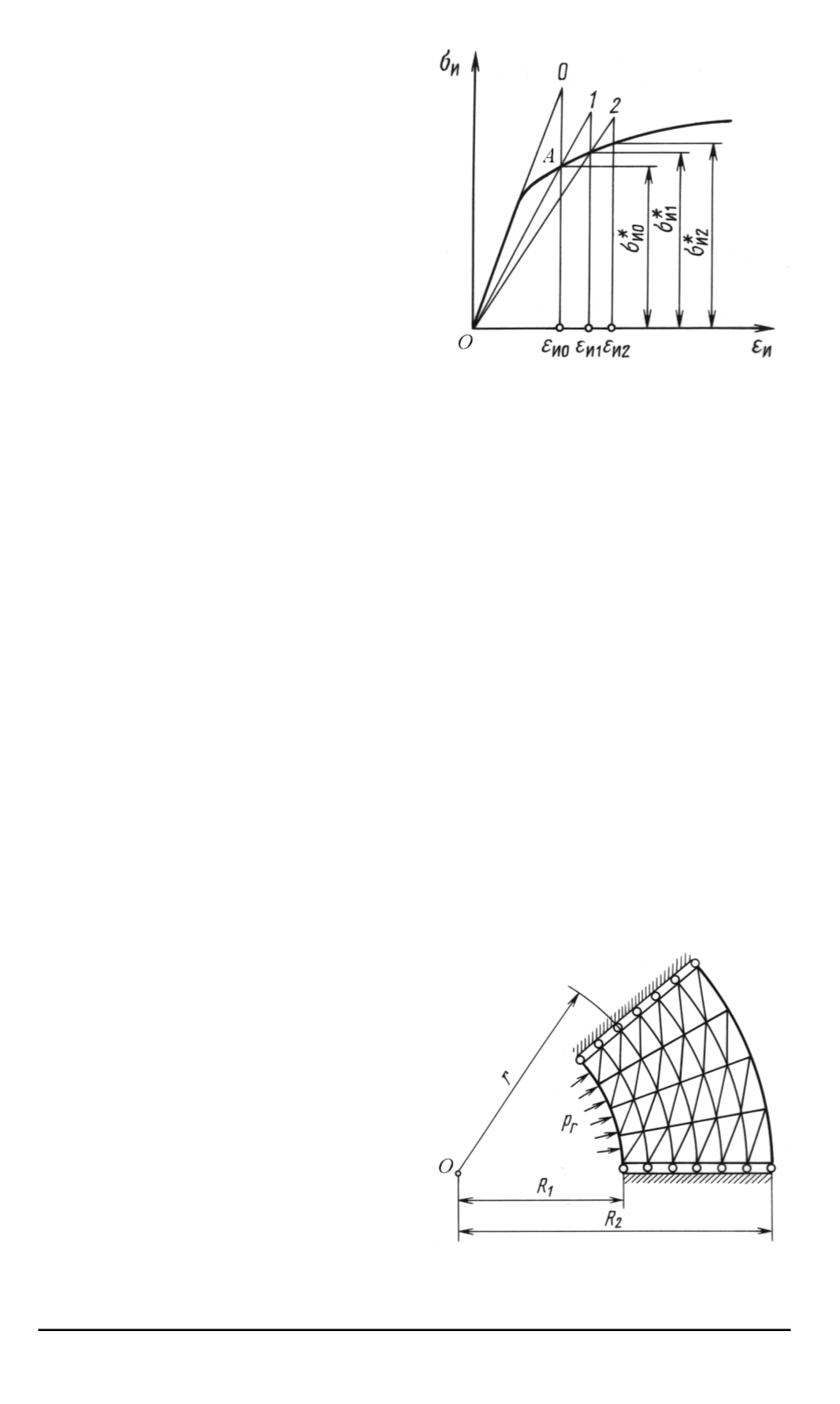
Рис
. 2.
Диаграмма деформирования
ε
и
0
по формулам
(18)
определяются
новые значения параметров
E
,
μ
и
G
,
которые будут различными в
различных элементах
.
Таким обра
-
зом
,
возникает задача определения
напряжений в неоднородном теле
.
Далее вновь методом локальных ва
-
риаций решается задача термоупру
-
гости
,
но уже с новыми параметра
-
ми
.
В результате решения находят
-
ся перемещения для первого при
-
ближения
.
Процесс коррекции па
-
раметров упругости продолжается
до тех пор
,
пока результаты двух последовательных приближений не
станут достаточно близки
.
Результаты численного решения
.
При численном решении зада
-
чи упругопластичности в качестве объекта рассматривалась цилиндри
-
ческая труба с радиусами
R
1
= 150
мм и
R
2
= 156
мм
.
Начальные
значения узловых перемещений соответственно в радиальном и окруж
-
ном направлениях были приняты равными
u
(0)
= 0
,
1
мм
,
v
(0)
= 0
мм
,
а начальные значения шагов варьирования соответственно в радиаль
-
ном и окружном направлениях были приняты равными
h
u
= 0
,
001
мм
,
h
v
= 0
,
0001
мм
.
Процесс варьирования завершался
,
когда шаги варьи
-
рования становились меньше
h
= 10
−
10
мм
.
Для решения этой задачи была построена конечноэлементная мо
-
дель
.
Для этого выделялся фрагмент поперечного сечения трубы
.
Вы
-
деленная часть разбивалась на слои изменяющимся радиусом
r
,
R
1
≤
≤
r
≤
R
2
,
и лучами
,
проходящими через центр поперечного сечения
,
а
затем еще на треугольники
(
рис
. 3).
Рис
. 3.
Конечноэлементная модель ци
-
линдрической трубы
Численные исследования про
-
водились для трех вариантов нагру
-
жения
.
В первом случае расчет прово
-
дился для трубы
,
находящейся под
воздействием внутреннего давле
-
ния
,
которое изменялось в диапа
-
зоне
p
г
= 2
,
1
. . .
2
,
5
МПа
.
Распре
-
деления радиальных и окружных
напряжений по толщине трубы
представлены на рис
. 4.
Из анализа
результатов следует
,
что при увели
-
чении значения внутреннего дав
-
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
93


