Рис
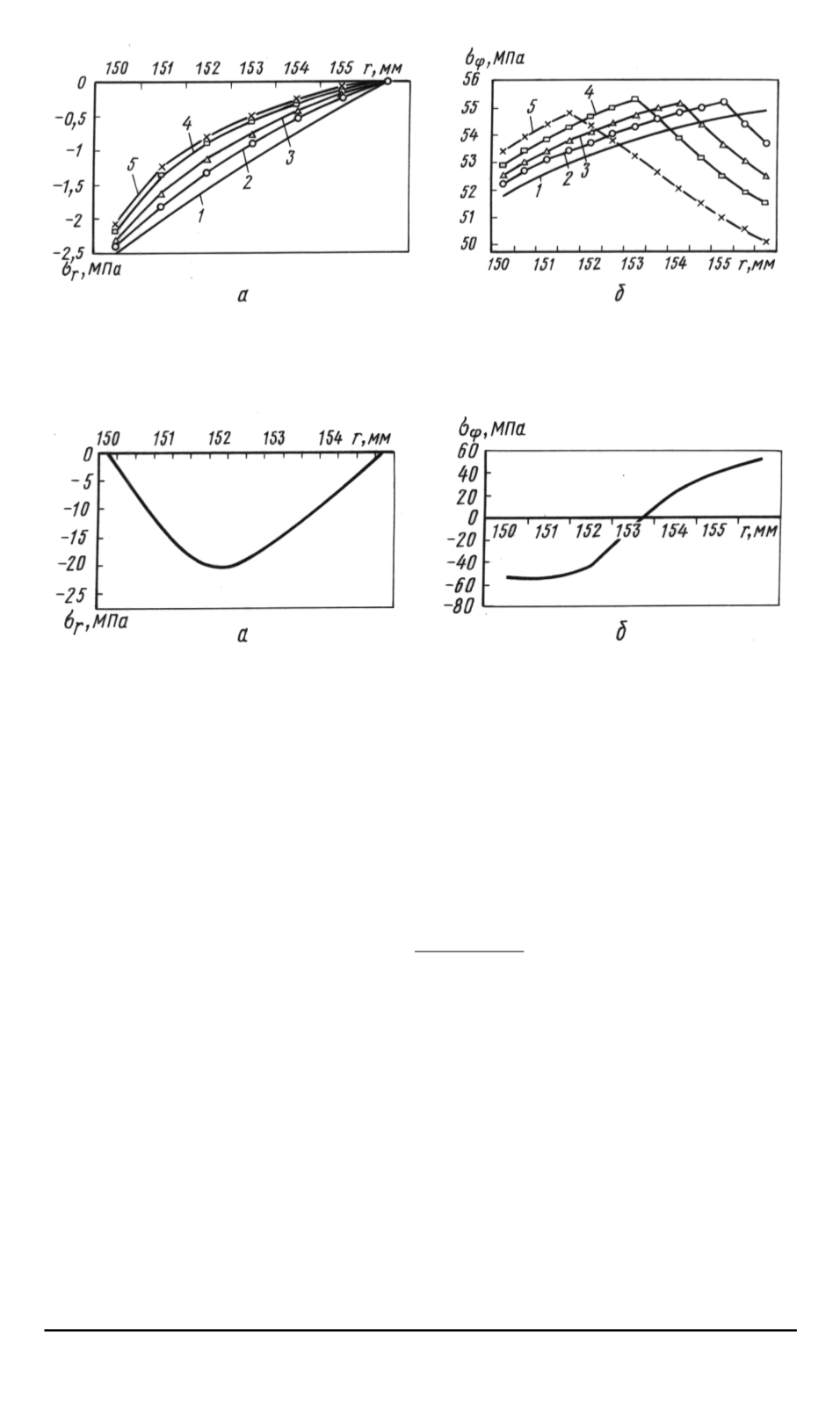
. 4.
Напряжения при действии внутреннего давления
:
а
—
радиальное напряжение
;
б
—
окружное напряжение
;
1
—
p
= 2
,
5
МПа
;
2
—
p
= 2
,
4
МПа
;
3
—
p
= 2
,
3
МПа
;
4
—
p
= 2
,
2
МПа
;
5
—
p
= 2
,
1
МПа
Рис
. 5.
Напряжения при температурном воздействии
:
а
—
радиальное напряжение
;
б
—
окружное напряжение
ления граница зоны пластичности
r
(
p
)
перемещается от внутреннего
радиуса
r
(
p
)
=
R
1
при
p
г
≈
2
,
1
МПа к внешнему радиусу
r
(
p
)
=
R
2
при
р
г
≈
2
,
5
МПа
(
рис
. 4,
б
).
Во втором случае рассматривалось напряженно
-
деформированное
состояние трубы под влиянием температурного поля
.
При этом темпе
-
ратура распределялась по радиусу трубы по логарифмическому закону
:
T
(
r
) =
T
b
ln(
R
2
/r
)
ln(
R
2
/R
1
)
,
где
T
b
= 150
◦
C —
температура на внутренней поверхности цилиндра
.
Графики изменения радиальных и окружных напряжений в зависимо
-
сти от радиуса показаны на рис
. 5.
В третьем случае труба была нагружена внутреннем давлением
(
p
г
= 2
МПа
)
и температурным полем
(
T
b
= 150
◦
С
).
Результаты реше
-
ния показаны на рис
. 6.
Заключение
.
Чтобы получить решение
,
требовалось выполнить
пять
-
шесть раз коррекцию параметров упругости
(
в соответствии с ме
-
тодом переменных параметров упругости
)
и реализовать около
10000
итераций методом локальных вариаций
.
Однако разработанный алго
-
ритм решения достаточно прост
,
легко программируется и не требует
94
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2


