Исследование коэффициента концентрации напряжений при
кручении прямолинейных анизотропных шлицевых валов
.
Рас
-
смотрим кручение шлицевых валов
,
материалы которых обладают пря
-
молинейной анизотропей
.
Как известно
,
решение задачи кручения прямолинейных анизо
-
тропных стержней сводится к решениям подобных задач для изо
-
тропных стержней
,
но не в области поперечного сечения
Ω
,
а в обла
-
сти
Ω
0
,
полученной аффинным преобразованием области
Ω
.
Зада
-
ча кручения изотропного стержня решается методом граничных ин
-
тегральных уравнений
(
ГИУ
).
Интегральные уравнения решаются
численно
-
аналитическим методом
(
методом последовательных при
-
ближений
) [1].
В научной литературе и справочных пособиях по машиностроению
указаны значения коэффициентов концентрации напряжений для от
-
дельных шлицевых валов с закругленными углами
[1].
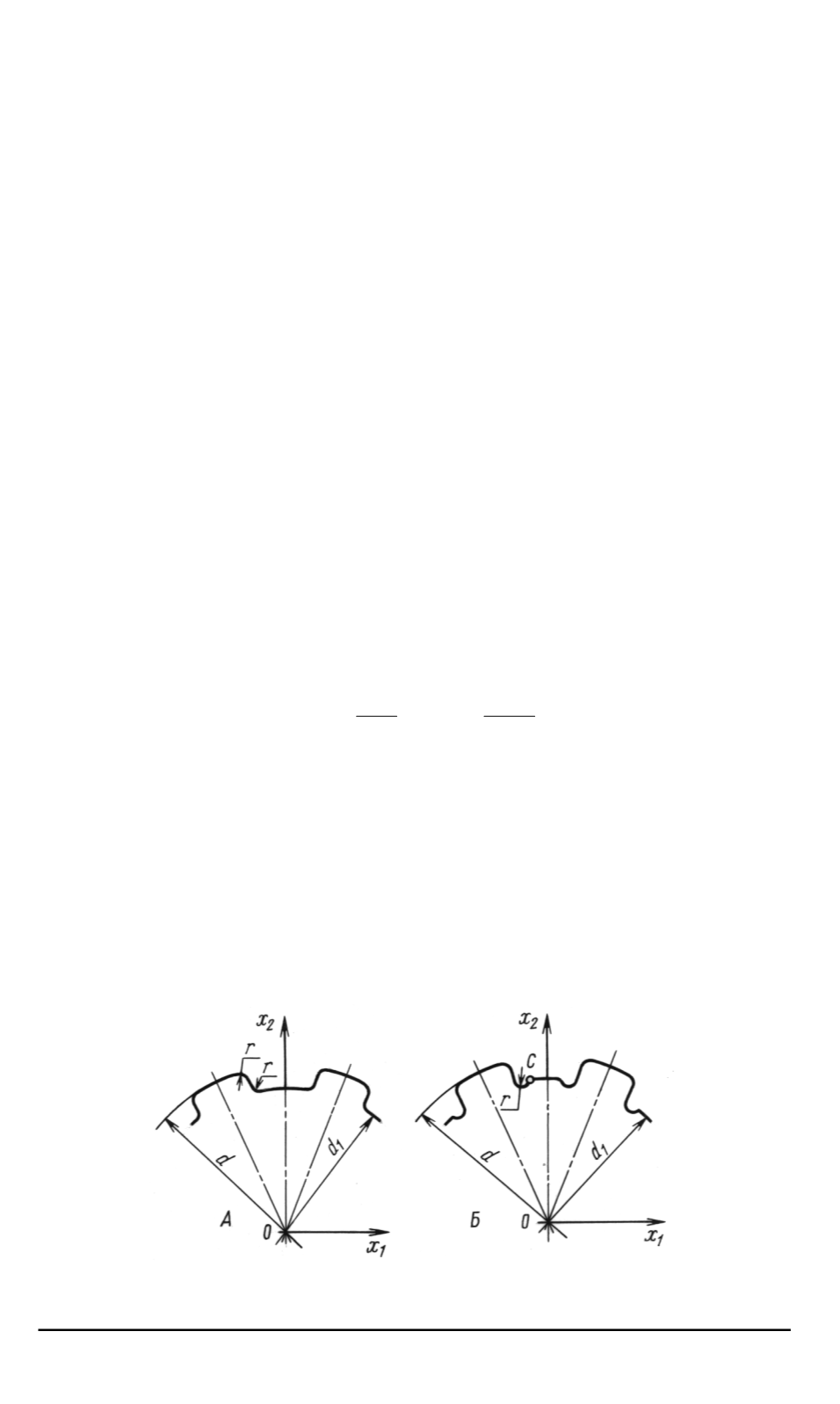
В данном разделе приводится решение ГИУ задачи кручения шли
-
цевых валов типов А и Б
,
показанных на рис
. 1.
Контур шлицевого вала относится к прямолинейной системе коор
-
динат
x
1
,
x
2
.
Координатные линии контура вала не совпадают с коор
-
динатными линиями прямолинейной анизотропии
.
Коэффициент концентрации определяется соотношением
K
ts
=
τ
max
τ
, τ
=
16
M
πd
3
,
(1)
где
M
—
крутящий момент
;
d
—
диаметр сплошного вала
,
совпадаю
-
щего со шлицевым валом по внешнему контуру
(
без учета шлицевых
выемок
);
τ
max
—
наибольшее по модулю напряжение
,
возникающее в
рассчитываемом вале
.
В табл
. 1
приведены результаты вычисления коэффициента кон
-
центрации напряжений и наибольшего касательного напряжения пря
-
молинейных анизотропных
(
при упругих постоянных
a
44
= 1
,
588
×
Рис
. 1.
Контуры шлицевых валов типов
A
и Б
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
97


