Исследование напряженного состояния анизотропных тел - page 5

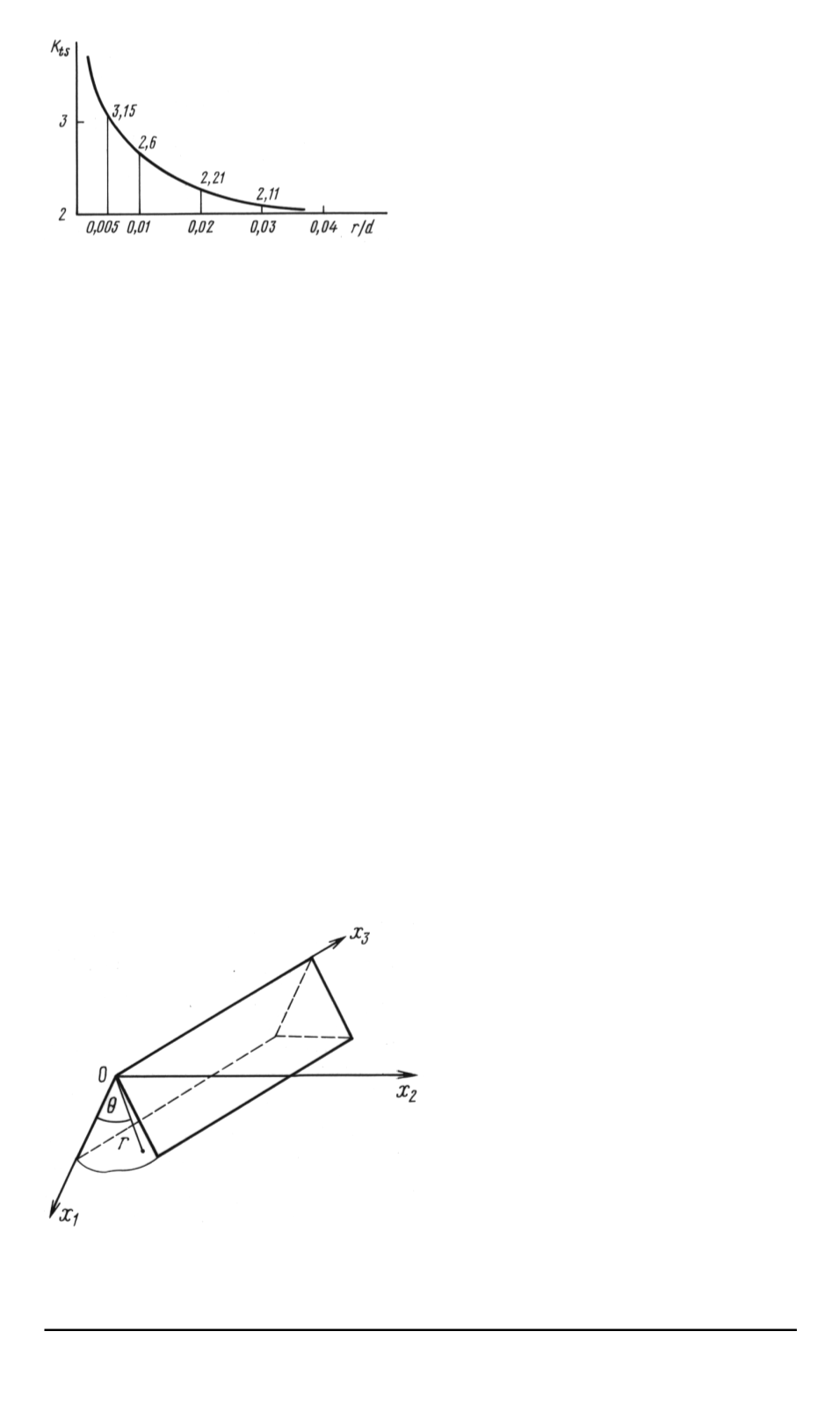
Рис. 4. Графики изменения коэффи- циента концентрации напряжений
для шлицевого вала типа А
неустойчивому счету и накоплению
ошибок из-за приближения точки C к боковой стороне зуба.
Проводимые выше решения за- дач кручения для шлицевых валов
с закругленными контурами при
сравнении с решениями задач кру- чения тех же валов с угловыми точ- ками на контуре сечения обладают
тем существенным отличием, что у
первых напряжения в опасных точках оказываются конечными, а у вто- рых — бесконечными. Одно важное обстоятельство объединяет эти ре- шения. Как доказано в [4], при замене гладкого контура с закругленны- ми углами на негладкий, с угловыми точками на контуре, коэффици- енты концентрации напряжений на сглаженных контурах стремятся к
коэффициентам концентрации напряжений на негладкой границе (пре- дельный случай — вблизи угловых точек ; см. рис. 4). Кроме того, всю- ду, за исключением окрестностей опасных точек , напряженные состо- яния почти совпадают.
Антиплоские задачи для анизотропных неоднородных клиньев. Решения антиплоской задачи для клиньев простые , но имеют суще- ственный недостаток, связанный с тем , что область, в которой реша- ется задача, не имеет замкнутой границы. Математическая постановка
таких задач не корректна. Их решение обращается в бесконечность при
некоторых углах раствора клина. Для этих углов напряжения имеют ло- гарифмическую особенность .
Рис. 5. Прямолинейный анизотропный
клин в системе цилиндрических коорди- нат
Антиплоские задачи для кли- ньев, обладающих прямолиней- ной анизотропией. Рассмотрим
в системе координат r, θ, x3 клин
(0 ≤ r < +∞, 0 ≤ θ ≤ α,
−∞ < x3 < +∞) (рис. 5), материал которого обладает пря- молинейной анизотропией , име- ющей одну плоскость упругой
симметрии . Предположим, что
одна грань клина закреплена , а
на другую приложены касатель- ные напряжения τ0 , параллель- ные образующей .
100 ISSN 1812-3368. Вестник МГТУ им. Н.Э . Баумана. Сер. “Естественные науки”. 2005. № 2